|
Question 54266This question is from textbook Algebra for College Students
: To solve for this equation, 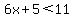 or or 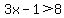 I would have to do the same to both sides correct? if I (-5) to the 11 side I must do the same to the 8 side right? From there I would solve for x normally and that gives me the 2 answers? I think I have the logic down, just need to make sure my steps are correct. I would have to do the same to both sides correct? if I (-5) to the 11 side I must do the same to the 8 side right? From there I would solve for x normally and that gives me the 2 answers? I think I have the logic down, just need to make sure my steps are correct.
Thank you
This question is from textbook Algebra for College Students
Found 3 solutions by Nate, stanbon, Edwin McCravy:
Answer by Nate(3500)   (Show Source): (Show Source):
Answer by stanbon(75887)   (Show Source): (Show Source):
Answer by Edwin McCravy(20060)   (Show Source): (Show Source):
You can put this solution on YOUR website! To solve for this equation,
6x+5 < 11 OR 3x-1 > 8
I would have to do the same to both sides correct?
if I (-5) to the 11 side I must do the same to the
8 side right? From there I would solve for x normally
and that gives me the 2 answers? I think I have the
logic down, just need to make sure my steps are
correct.
Thank you
-----------------------------------------------------
First of all that is a two-part inequality, not an
"equation".
Solve each part separately
6x + 5 < 11 OR 3x - 1 > 8
-5 -5 +1 +1
----------------------------
6x < 6 OR 3x > 9
Divide both sides of first by 6
Divide both sides of second by 3
x < 1 OR x > 3
Graph: Since x can be either
left of 1 or else right of 3, we
shade everwhere x can be:
<==============o-----o==========>
-3 -2 -1 0 1 2 3 4 5 6
Interval notation: (-oo, 1) U (3, oo)
Edwin
|
|
|
| |