Question 541690: Three student representatives, a president, a secretary, and a treasurer, are to be chosen from a group of five students: Andrew, Brenda, Chad, Dorothy, and Eric. In how many different ways can the representatives be chosen if the president must be a woman and the secretary and treasurer must be men?
My answer is 6, but it's not correct. The correct answer is 12. I don't know why "12".
Answer by neatmath(302)   (Show Source): (Show Source):
You can put this solution on YOUR website!
This is one of those counting method problems, using the multiplication principle.
In this case, we have very specific rules for selecting the representatives.
There are 3 positions, how many ways can we "choose" each position?
In the first slot, we can only place a woman, so we have 2 choices.
In the second slot, we can only place a man so we have 3 choices.
In the third slot, we can only place a man (who wasn't already chosen), so we have ONLY 2 choices.
This because we assume one person can't be both the secretary and the treasurer at the same time.
Then we just need to multiply the number of choices!
In this case we have
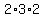
which equals 
I hope this helps!
|
|
|