SOLUTION: The positive integers 30, 72, and N have the property that the product of any two of them is divisible by the third. What is the smallest possible value of N?

Algebra ->  Problems-with-consecutive-odd-even-integers -> SOLUTION: The positive integers 30, 72, and N have the property that the product of any two of them is divisible by the third. What is the smallest possible value of N?      Log On


   

Question 541373: The positive integers 30, 72, and N have the property that the product of any two of them is divisible by the third. What is the smallest possible value of N?
Answer by Edwin McCravy(20056) About Me  (Show Source):
You can put this solution on YOUR website!
30, 72, and N

There must exist positive integers A, B, and C such that 

30·72 = NA
  30N = 72B
  72N = 30C

Simplifying:

2160 =  NA
  5N = 12B
 12N =  5C  

Solving each for N:

N = 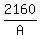2160%2FA
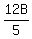N = 12B%2F5
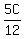N = 5C%2F12

Set the last two right sides equal, since both are equal to N

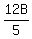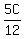12B%2F5 = 5C%2F12

144B = 25C

The smallest B and C can be are B = 25 and C = 144

Substituting in

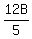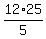N = 12B%2F5 = 12%2A25%2F5 = 60 
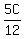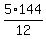N = 5C%2F12 = 5%2A144%2F12 = 60

That works because

30, 72, and 60

30*72 = 2160 = 60*36
30*60 = 1800 = 73*25
60*72 = 4320 = 30*144

So the answer is N = 60

Edwin