SOLUTION: Find an acute angle θ that satisfies the equation. sin⁡θ=cos⁡2θ+60°) tip: (sin⁡θ=cos⁡(90-θ))

Algebra ->  Trigonometry-basics -> SOLUTION: Find an acute angle θ that satisfies the equation. sin⁡θ=cos⁡2θ+60°) tip: (sin⁡θ=cos⁡(90-θ))       Log On


   

Question 541147: Find an acute angle θ that satisfies the equation.
sin⁡θ=cos⁡2θ+60°)
tip: (sin⁡θ=cos⁡(90-θ))
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
sin%28theta%29=+cos%282theta%2B60%29
With the tip, it transforms into
cos%2890-theta%29=cos%282theta%2B60%29
If two angles are the same, they have the same cosine.
So at least we'll get a solution from 90-theta=2theta%2B60
Adding theta to both sides, we get 90=3theta%2B60
Subtracting 60 from both sides, we get 30=3theta
Dividing both sides by 3, we get 10=theta
So theta=10degrees is a solution.
Are there others?
Could the cosines be equal, but the angles be different?
In general, that could happen, but since theta is an acute angle
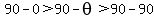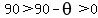
0%3Ctheta%3C90 --> 90-0%3E90-theta%3E90-90 --> 90%3E90-theta%3E0
So 90-theta; is an acute angle too. That means its cosine is a positive number.
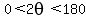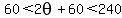
0%3Ctheta%3C90 --> 0%3C2theta%3C180 ---> 60%3C2theta%2B60%3C240
The angle 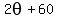2theta%2B60 seems to have more options, but since its cosine is equal to a positive number, it is more restricted.
The only cosines that area positive for angles between 60° and 240° are those for angles between 60° and 90°. Between 90° and 270° they are negative.