Question 541145: Hello;
I am in a college beginning algebra class and I am struggling with solving equations by addition method here are the problems I am having problems with, I am hoping you can help me by showing the work to explain the process.
1) x+2y=6
x-y=3 solve by addition method with an answer for (x,y)
2)4x-5y=22
x+2y=-1 do the same by solving by addition method and an answer for (x,y)
3) 4x-5y=-3
-3x+2y=4 also solve by addition method for an answer for (x,y)
Thank you very much for your time, I hope you can help!
-Ashley
Found 2 solutions by friesr, MathTherapy:
Answer by friesr(113)   (Show Source): (Show Source):
You can put this solution on YOUR website! 1) x+2y=6
2y = -x + 6
y = -x/2 + 3
2)4x-5y=22
5y = -4x +22
y = -4/5 x + 22/5
3) 4x-5y=-3
5y = -4x -3
y = -4/5x - 3/5
x-y=3
-y = -x +3
y = x-3
x+2y=-1
2y=-x - 1
y= -x/2 -1/2
-3x+2y=4
2y = 3x + 4
y = 3/2x + 2
Not sure if this is what you are looking if not, let me know.
Answer by MathTherapy(10552)   (Show Source): (Show Source):
You can put this solution on YOUR website! Hello;
I am in a college beginning algebra class and I am struggling with solving equations by addition method here are the problems I am having problems with, I am hoping you can help me by showing the work to explain the process.
1) x+2y=6
x-y=3 solve by addition method with an answer for (x,y)
2)4x-5y=22
x+2y=-1 do the same by solving by addition method and an answer for (x,y)
3) 4x-5y=-3
-3x+2y=4 also solve by addition method for an answer for (x,y)
Thank you very much for your time, I hope you can help!
-Ashley
1)
x + 2y = 6 ----- eq (i)
x - y = 3 ------ eq (ii)
- x - 2y = - 6 ----- Multiplying eq (i) by - 1 ----- eq (iii)
- 3y = - 3 ------ Adding eqs (iii) & (ii)
y = 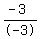 , or , or 
x + 2(1) = 6 ------ Substituting 1 for y in eq (i)
x + 2 = 6
x = 6 - 2, or 
I'm not familiar with the addition method and would assume that this method is just that. This method is known as the ELIMINATION method and involves the addition or subtraction of the two equations from one another, after being altered.
You can now try the other two by following the same concept. If not successful, write again, and someone might help.
Send comments and “thank-yous” to "D" at MathMadEzy@aol.com
|
|
|