Question 540981: Find x given 30-60-90 triangle and the length 18 on one side and x length of the other side simplified radical
Answer by KMST(5328)   (Show Source):
You can put this solution on YOUR website! I don't know if the short leg is the side with length 18, or if it is the long leg. I'll try it both ways, then.
A 30-60-90 triangle is a right triangle that could be half of an equilateral triangle. In the figure below, triangles APC and PBC are congruent halves of equilateral triangle ABC. You could fold equilateral triangle ABC down the middle along altitude CP and vertices A and B would be superimposed.
For triangle PBC, if the length of long leg CP was 18, I would call the length of AP x, and the lenghts of AB, BC, and AP would all be 2x.
Calling the other leg (altitude CP) x, we can write (from Pythagoras theorem)
 -->  -->  -->  --> 
Since the length of a segment cannot be a negative number, the only solution is
For triangle PBC, if the length of short leg BP was 18, the length of AP would also be 18, and the lenghts of AB, BC, and AP would all be 36.
Calling the other leg (altitude CP) x, we can write (from Pythagoras theorem)
 -->  --> 
Since the length of a segment cannot be a negative number, the only solution is
NOTE:
It is a fact that the ratio of the sides' lengths in all 30-60-90 triangles is 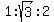 . If you were taught that fact in class and are allowed to refer to it, you could just use it, and the and calculations would be easier.
|
|
|
