|
Question 540835: Determine the quadratic function, f(x) = ax^2 + bx + c, whose vertex is (1, 8) and passes through the point (-3, 4)
Answer by AnlytcPhil(1806)   (Show Source):
You can put this solution on YOUR website! Determine the quadratic function, f(x) = ax^2 + bx + c, whose vertex is (1, 8) and passes through the point (-3, 4)
It has the form
f(x) = a(x - h)² + k where the vertex is (h,k),
Since we are given that the vertex is (1,8), we have
f(x) = a(x - 1)² + 8
Since the parabola passes through the point (x,y) = (-3,4), we will
substitute -3 for x and since y = f(x) we will substitute 4 for f(x):
4 = a(-3 - 1)² + 8
4 = a(-4)² + 8
4 = a(16) + 8
4 = 16a + 8
-4 = 16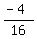a
 = a
 = a
We substitute for a in
f(x) = a(x - 1)² + 8
f(x) = (x - 1)² + 8
That is in vertex form. To get it in standard form f(x) = ax² + bx + c
f(x) = (x - 1)(x - 1) + 8
f(x) = (x² - 2x + 1) + 8
f(x) = x² - ·2x + ·1 + 8
f(x) = x² +  x -  + 8
f(x) = x² + x - + 32/4
f(x) = x² + x +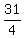 
Edwin
|
|
|
| |
