Question 537280: I need help with this please:
Given that a two-digit number is randomly selected, what is the probability that the sum of the digits exceeds five? Express your answer as a common fraction.
Answer by josmiceli(19441)   (Show Source): (Show Source):
You can put this solution on YOUR website! Let P stand for probability
( P that sum of digits exceeds 5 ) + ( P that sum is 5 or less ) = 1
The probabilities of everything that can possibly happen
must add up to one, therefore:
( P that sum of digits exceeds 5 ) = 1 - ( P that sum is 5 or less )
The 2 digit numbers that are 5 or less are
10,11,12,13,14
20,21,22,23
30,31,32
40,41
50
There are 15 of these numbers
The sum of digits of all the other 2 digit numbers exceed 5
The tens digit can be 1 - 9, or 9 possible
The units digit can be 0 - 9 or 10 possible
Total possible numbers = 
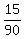 = P that sum is 5 or less = P that sum is 5 or less



P that sum of digits exceeds 5 = 5/6
|
|
|