Question 537174: The problem is... solve the equation on the interval 0 less than/equal to theta and 2pi is greater than theta... and the equation is 2sqrt(3) sin (4theta) = 3
interval 0≤θ<2π
2√ 3 sin (4θ) = 3
The answers that the book got were { pi/12, pi/6, 2pi/3, 7pi/6,13pi/12, 5pi/3, 19pi/12}... and I want to know how they got those answers please (step by step would be great)
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website!  --> --> 
 --> -->
Teachers like to give students a chart, or better yet a printed circle, with the angle measurements and exact values for sine, cosine, tangent for certain notable angles, so that number may ring a bell. You do not need to memorize them, or have the chart because they all derive from Pythagoras theorem and triangles that are half of a square or half or an equilateral triangle. However, having such a chart helps keep your calculations straight.
You should know that  (60 degrees) is one answer (sine and cosine of 30, 45, and 60 degrees are well known values). (60 degrees) is one answer (sine and cosine of 30, 45, and 60 degrees are well known values).
 is another solution (180-60=120 degrees, the supplementary angle has the same sine). You find more (coterminal) solutions for is another solution (180-60=120 degrees, the supplementary angle has the same sine). You find more (coterminal) solutions for 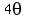 in the next turn, and the next, and the next> You can find the coterminal in the next turn, and the next, and the next> You can find the coterminal 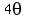 solutions by adding to the two solutions above solutions by adding to the two solutions above  (360 degrees), (360 degrees),  , and , and  to get a total of eight values for to get a total of eight values for 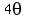 : :
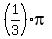 , ,  , , 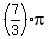 , , 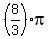 , , 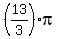 , , 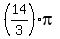 , , 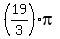 , and , and 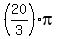 . .
Dividing by 4, we get the values for 
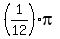 , ,  , , 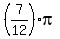 , ,  , , 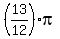 , ,  , , 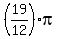 , and , and  . .
|
|
|