SOLUTION: if you have a triangle with sides of 60cm, base of 63cm height of 36cm and you have to solve for X which is the other side how do you do it?

Algebra ->  Polynomials-and-rational-expressions -> SOLUTION: if you have a triangle with sides of 60cm, base of 63cm height of 36cm and you have to solve for X which is the other side how do you do it?      Log On


   

Question 536661: if you have a triangle with sides of 60cm, base of 63cm height of 36cm and you have to solve for X which is the other side how do you do it?
Answer by fcabanski(1391) About Me  (Show Source):
You can put this solution on YOUR website!
Essentially this problem specifies the area of the triangle, A=%281%2F2%29bh+=+%281%2F2%2963%2A36=1134 and two sides.


When given the area and two sides of a triangle use Heron's Formula which states.


where a, b and c are the three sides of the triangle.


Call a=60cm, b=63cm and c the unknown side.


Let's try to simplify that right side before substituting what we know for a and b.




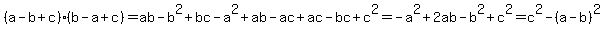
Multiply both sides by 16 to remove the denominator on the right. That makes the equation:


20575296=%28%28a%2Bb%29%5E2-c%5E2%29%28c%5E2-%28a-b%29%5E2%29


Substitute the values we know:



Set x=c%5E2 and rewrite the equation.


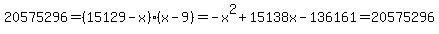
20575296=%2815129-x%29%28x-9%29=-x%5E2%2B15138x-136161=20575296


Subtract 20575296 from both sides.


-x%5E2%2B15138x-20711457=0


Multiply both sides by -1.


x%5E2-15138x%2B20711457=0


Maybe the Rain Man could factor that, but we'll have to use the quadratic equation to find x, then take the square root of x to find c.


x+=+%28-b+%2B-+sqrt%28+b%5E2-4%2Aa%2Ac+%29%29%2F%282%2Aa%29 =


%2815138+%2B-+sqrt%28%28-15138%29%5E2-4%2A1%2A20711457%29%29%2F%282%2A1%29 =


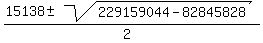%2815138+%2B-+sqrt%28229159044-82845828%29%29%2F%282%29=


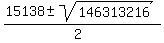%2815138+%2B-+sqrt%28146313216%29%29%2F%282%29=


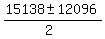%2815138+%2B-+12096%29%2F%282%29=


That gives x=%2815138%2B12096%29%2F2 and x=%2815138-12096%29%2F2


x=13617 and x=1521


So c=sqrt%2813617%29=116.69and c=sqrt%281521%29=39


Both will work. To prove it, plug into another version of Heron's Formula which is:


A+=+sqrt%28s%28s-a%29%28s-b%29%28s-c%29%29


Where a, b and c are the sides, and s is the semiperimeter and s+=+%28a%2Bb%2Bc%29%2F2


For c=116.69 this is:


s+=+%2860%2B63%2B116.69%29%2F2=119.85


A+=+1134=+sqrt%28119.85%28119.85-60%29%28119.85-63%29%28119.85-116.69%29%29=


A+=+1134=+sqrt%28119.85%2859.85%29%2856.85%29%283.16%29%29=


A+=+1134=+sqrt%281286291.58%29=1134%29


For c=39 this is:


s+=+%2860%2B63%2B39%29%2F2=81


A+=+1134=+sqrt%2881%2881-60%29%2881-63%29%2881-39%29%29=


A+=+1134=+sqrt%28119.85%2821%29%2818%29%2842%29%29=


A+=+1134=+sqrt%281285956%29=1134%29


If you need help understanding math so you can solve these problems yourself, then one on one online tutoring is the answer ($30/hr). If you need faster solutions with guaranteed detailed answers, then go with personal problem solving ($3.50-$5.50 per problem). Contact me at fcabanski@hotmail.com