Question 536595: Here is another way to determine the number of solutions for a system of equations, using ratios. Please show how to apply it on the system at the bottom:
The system of equations a1x + b1y + c1 = 0, a2x + b2y + c2= 0 has:
A unique solution if a1/a2 ≠ b1/b2
No solution if a1/a2 = b1/b2 ≠ c1/c2
An infinite number of solutions if a1/a2 = b1/b2 = c1/c2
This is a very helpful test to quickly determine the nature of your system. Please demonstrate how you would apply it on this system:
y - 3 = x
2y - 2x = 6
Please help, I am not even sure I understand what my teacher is asking of me!
Answer by bucky(2189)   (Show Source):
You can put this solution on YOUR website! Here is what your teacher is asking you to do.
.
If you are given two equations, each involving x, y, and a constant, rearrange each of the two equations as necessary to get both of them into the form:
.
 and
.
Note that if you're really good at working what the teacher wants you to do, you don't have to rearrange the two equations. But if you don't rearrange them into the form above, it's easy to make a mistake. So I would rearrange the equations into the above form.
.
Next find the following ratios:
.
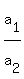 an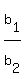d  and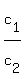 
.
Then look at the two ratios, the first for the a's and the second for the b's. If these two ratios are unequal, then the two equations have one common solution. The reason for this is that if these two ratios are unequal, the graphs for the two equations have different slopes and therefore the graphs will cross at a single point known as the common solution.
.
But if the two ratios for the a's and the b's are equal, then the graphs have the same slope. This means that there are two possibilities: either the graphs are not on top of each other and are parallel lines or the two graphs lie on top of each other so they have an infinite number of solutions. The first possibility happens if the ratio of the c's does not equal the ratio of the a's or the b's. The second possibility (an infinite number of common solutions) happens if the ratio of the c's equals the ratio of the b's and the ratio of the a's.
.
Given this, let's look at the problem the teacher gave you and see how to work it out. Given the two equations:
.
The first equation is  and
the second equation is 
.
Let's rearrange the first equation by subtracting x (or adding a negative x) to both sides. On the right side the x and the negative x we add cancel each other out and we are left with zero on the right side. The rearranged first equation becomes:
.
.
Note that the multiplier of the x is  . Note that the multiplier of the y is  and finally the constant is 
.
Now lets rearrange the second equation. On the left side we just switch the order of the 2y and the -2x. This makes the second equation become:
.
.
Then we subtract 6 from both sides and the equation is then in the form that we want. That form is:
.
.
Notice that for this equation the multiplier of the x is  and the multiplier of the y is  and finally the constant is  .
.
Let's review. For the first equation we have and and . For the second equation we have and and .
.
Now let's find the ratio of the a's.  and this reduces to  .
.
Next the ratio of the b's.  .
.
Finally, let's find the ratio of the c's.  and that simplifies to 
.
What can we now tell about these two equations? First we know that that they don't have a single common solution. To have a single common solution the ratio of the a's (which we found was 1/2) must be different from the ratio of the b's (which we found was also  . Since these two ratios are the same, we know that the graphs of the two equations are parallel lines.
.
So next we look at the ratios of the c's. We found that ratio to be . Therefore, it is equal to the ratios of the a's and b's. That tells us that there is an infinite number of solutions and the graphs of the two equations lie on top of each other. If the ratios of the c's had also been a number other than 1/2, then we could say that the graphs of the two equations were separate but parallel lines and there was no common solution.
.
This ratio method is just another way of doing a slope intercept analysis. I like to get the two equations into the slope intercept form of:
.
.
If you put both equations into this form, you can compare slopes (the multiplier of the x) and the y-intercepts and tell the same things as the ratios tell you. If the slopes are unequal, there is one common solution. If the slopes are equal, then look at the constants (the b's). If they are different then you have parallel lines and no common solution. If the constants are the same then you have the same graphs so that there are an infinite number of common solutions.
.
Let's work the problem you were given, only this time we'll use the slope intercept form.
.
The first equation you were given was:
.
.
Put this into slope intercept form by adding +3 to both sides and you have that the first equation is:
.
.
Now for the second equation. You were given:
.
.
Add 2x to both sides to change this equation to:
.
.
Solve for y by dividing both sides (all terms) by 2 to get:
.
.
Notice that this slope intercept form is identical to the slope intercept equation for the first equation. The two lines have the same slope ... it is +1 because it is the multiplier of the x. They also cross the y-axis at the same point (the constant +3). Therefore, they graph as the same line and they have an infinite number of common solutions, just as we found by analyzing the three ratios.
.
Hope this helps you to understand the problem and the lesson that your teacher was trying to familiarize you with.
.
|
|
|
