Question 535981: One solution of kx^2-5x+k=0 is 3. Find the other solution
Answer by bucky(2189)   (Show Source): (Show Source):
You can put this solution on YOUR website! Problem: if one solution of the quadratic equation:
.

.
is 3, what is the other solution?
.
Notice that when you term-by-term compare the given equation to the standard form of the quadratic equation:
.

.
you can see that "a" correlates to k, "b" equals -5, and "c" also equals k.
.
We know that the quadratic formula applies to solving a quadratic equation in the standard form. The quadratic formula says that for a quadratic equation in the standard form x can be found from:
.

.
into this formula we can substitute k for "a" and "c" and -5 for "b" to get:
.

.
The 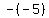 becomes + 5 and the becomes + 5 and the  and and  . These actions result in: . These actions result in:
.

.
multiply both sides by 2*k which is the denominator on the right side. This clears the denominator, and the formula becomes:
.

.
we also know that one value for x is 3. We were told that in the statement of the problem. So substitute 3 for x in the formula. This makes the left side become:
.

.
multiply out the left side to get:
.

.
get rid of the 5 on the right side by subtracting 5 from both sides:
.

.
square both sides to get rid of the radical on the right side and this formula becomes:
.

.
cancel 25 on both sides of the formula by subtracting 25 from both sides. Also get rid of the  on the right side by adding on the right side by adding 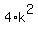 to both sides to get: to both sides to get:
.

.
Factor a k from terms on the left side:
.

.
notice that this equation will be true if either of the two factors on the left side is equal to zero because multiplication by a zero results in the left side becoming zero and making the left side equal to the zero on the right side.
.
So this formula will be true if either k = 0 or if 40k - 60 = 0. We can ignore k = 0 because if this were true in the original quadratic equation of the problem if k were zero, both the 
.
then dividing both sides by 60:
.

.
and reducing the right side by dividing both the numerator and denominator by 20 to get:
.

.
Now we can go back to the original problem and substitute  for k to make it become: for k to make it become:
.

.
Multiply all terms by 2 to cancel out the denominator and you have:
.

.
compared to the standard quadratic equation we now have "a" = 3, "b" = -10, and "c" = 3. Substituting these values into the quadratic formula, we get:
.

.
which becomes:
.

.
Simplifying to:
.

.
The radical term becomes the square root of 64:
.

.
which simplifies to:
.
 and this simplifies to and this simplifies to 
.
and
.
 and this simplifies to and this simplifies to 
.
The first value for x we already knew because it was part of the problem. The second value for x, which we found was  , is the answer you were asked to find in the problem. , is the answer you were asked to find in the problem.
.
Hope this helps you to understand the quadratic equation a little better and how to apply that knowledge to solving this problem.
.
Check my work. It's late and I might have introduced some errors due to lack of coffee. You can also check this problem by multiplying the two factors:
.
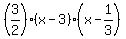 and see if the answer does not give you the original equation in the problem in which and see if the answer does not give you the original equation in the problem in which 
.
Good luck ...
.
|
|
|