Question 535908: Find the LCM. 21a^3b^8, 3a^3b^2, 14a^3b^5. I know part of the answer is 42, but I am completely stuck on the rest. I came up with 42 3/6, but I think it is wrong.
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! If I understand the question, the trio of monomials we have is
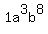 , , 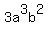 , , 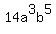
We need a multiple of the three, the least of them, the least common multiple, affectionately called the LCM.
It needs to be a multiple of the number part, the coefficients 1, 3, and 14, so you are right that you need a 42 in your answer.
Factors a an b represent variables, so for a multiple of  , we need , we need  as a factor, and for a multiple of as a factor, and for a multiple of 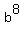 , we need , we need 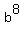 as a factor. We include all the factors, with the highest exponent seen in the monomials given. as a factor. We include all the factors, with the highest exponent seen in the monomials given.
We end up with 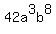 which is a common multiple because it can be written as a product of each of the monomials times other factors. which is a common multiple because it can be written as a product of each of the monomials times other factors.

It is the least common multiple because if we left out any of the factors we included (or we made the exponents smaller) it would fail to be multiple for at least one of the three monomials.
|
|
|