Question 535799: Factor completely,
11x(4x-3)-6(4x-3)=
2x(x-5)-(x-5)
3x^3-4x^2+6x-8=
xy+2x-y-2=
2x^2+2x-24=
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! 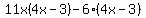 has a common factor, present in both terms. Getting that common factor out is applying the distributive property backwards, like this has a common factor, present in both terms. Getting that common factor out is applying the distributive property backwards, like this

 Same thing here Same thing here

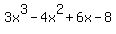 This polynomial is best factored by grouping. There are four terms. Look for a factor common to two of those terms, like This polynomial is best factored by grouping. There are four terms. Look for a factor common to two of those terms, like 
and a factor common to the other two terms. If the polynomial was an exercise in factoring, it should work. (just don't expect it to work for every polynomial.

Do you see now another common factor? Keep factoring.
 and that's your polynomial fully factored. and that's your polynomial fully factored.
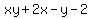 is another 4-term factor-by-grouping problem. By the way, there are two ways to group. They both work (unless you make a mistake). You may see only one way, but that would be enough. is another 4-term factor-by-grouping problem. By the way, there are two ways to group. They both work (unless you make a mistake). You may see only one way, but that would be enough.

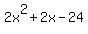 is a tougher factoring problem. If it can ve facored with nice integer numbers, it's going to end up being is a tougher factoring problem. If it can ve facored with nice integer numbers, it's going to end up being
 with with 
That gives you a bunch of choices for a and b because there are several pairs if factors whose products yield 24, and then you have a choice of which one to give the minus sign to. You know that the product term in x is
 , so , so 
I would try pairs like 3 and 8 (3x8=24) or 4 and 6 (4x6=24) rather than 2 and 12 or 1 and 24, because you need to add to 2, which is a small number.
Trying 8 and -3: 2x8-3=13 does not work,
but 2x(-3)+8=2 does. Lucky first guess!
Let's verify
 We got it! We got it!
|
|
|