Question 5357: I am having trouble understanding how to use the Perfect Square Trinomial Formula. my problem is:
9(x-3)^2-24(x-3)+16
I really don't even know where to begin. I have the formula:
a^2+2ab+b^2=(a+b)^2
a^2-2ab+b^2=(a-b)^2
Where do I go from here?
Answer by longjonsilver(2297)   (Show Source): (Show Source):
You can put this solution on YOUR website! if you do not understand factorisation, then attempting to factorise 9(x-3)^2-24(x-3)+16 is pointless for you, as it is several steps up from "basic".
The 2 "formulae" you quoted are a start, but you need to understand exactly what you are trying to do, so here goes...
y= x^2 +6x + 8 is a quadratic, ie it is a u-shaped curve. Now, this u-shaped curve may well cross the x-axis when you plot it. The point(s) that any curve crosses the x-axis are called the solutions or roots of the equations and it is these points that a lot of algebra is concerned with.
How do we find where the equation crosses the x-axis? Well the x-axis is the line y=0, since every point on the x-axis has y equal to zero. So, we have  , and we want to know the x-values when y=0, ie we want to find , and we want to know the x-values when y=0, ie we want to find 
Now, writing the equation this way doesn't help us. However, writing the equation as (one thing)*(another thing) is VERY helpful, since it equals zero remember: we now have 2 "things" multiplied that equal zero.
2x3? ...nope --> that is 6
-3x4? ...nope --> that is -12
-1x-7? ...nope --> that is +7
how about 0x56? ...YES --> that is 0. In other words, 2 things multiplied together...one of them MUST be zero. Which one? either could be.
So that is why we factorise: ie convert something to 2 things multiplied together.
So... factorise 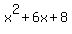 , well a general "formula" is: , well a general "formula" is:
(x+a)(x+b) = x^2 + (a+b)x + ab
So, we need 2 numbers such that they multiply to give the constant value (ab) and add together to give the coefficient of the x term.
 --> we need 2 numbers that multiply to give +8 and also add to give +6. --> we need 2 numbers that multiply to give +8 and also add to give +6.
Start off by writing down all the factors of 8 you know:
1x8
2x4
that is it..which of these pairs add to give 6? 2 and 4 Voila!
(x+2)(x+4) is the factorised version of 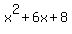 . Check this by multiplying out the 2 brackets... . Check this by multiplying out the 2 brackets...
Anyway, we have (x+2)(x+4) = 0, so we then know that x+2=0 OR x+4=0.
So, x=-2 or x=-4...the 2 answers we need.
Right, now back to your question...

lets just write y instead of x-3...to make it easier to see: 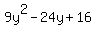 . Also, I shall write the 9 and 16 as squares: . Also, I shall write the 9 and 16 as squares: 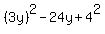 . Now can you see from your . Now can you see from your  formula that what we have now is VERY similar?... a is 3y and b is 4 (and 2ab does indeed equal 24y). So, we can factorise the equation to formula that what we have now is VERY similar?... a is 3y and b is 4 (and 2ab does indeed equal 24y). So, we can factorise the equation to 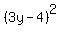 ie (3y-4)(3y-4). ie (3y-4)(3y-4).
Now, we just put the x back in... 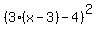 . This is the answer. Check by multiplying out the 2 brackets that you get back to the original question. . This is the answer. Check by multiplying out the 2 brackets that you get back to the original question.
Hope this has helped?
jon.
|
|
|