SOLUTION: A man travels 370 KM partly by train and partly by car. If he covers 250 KM by train and the rest by car. it takes him 4 Hours. But if he travels 130 KM by train and rest by car.

Algebra ->  Customizable Word Problem Solvers  -> Travel -> SOLUTION: A man travels 370 KM partly by train and partly by car. If he covers 250 KM by train and the rest by car. it takes him 4 Hours. But if he travels 130 KM by train and rest by car.       Log On

Ad: Over 600 Algebra Word Problems at edhelper.com


    

Question 535570: A man travels 370 KM partly by train and partly by car. If he covers 250 KM by train and the rest by car. it takes him 4 Hours. But if he travels 130 KM by train and rest by car. he taken 18 minut longer. Find the speed of the train and that of the car.
Found 2 solutions by mananth, MathTherapy:
Answer by mananth(16946) About Me  (Show Source):
You can put this solution on YOUR website!

250/x + 120/y =4
substitue 1/x with a & 1/y with b
250a+120b=4
130/x + 140/y = 4.3
130a+140b=4.3
250 a + 120 b = 4 .............1
130 a + 140 b = 4.3 .............2
Eliminate y
multiply (1)by -7
Multiply (2) by 6
-1750 a -840 b = -28
780 a + 840 b = 25.8
Add the two equations
-970 a = -2.2
/ -970
a = 0.00227
plug value of a in (1)
250 a + 120 b = 4
0.57 + 120 b = 4
120 b = 4 -0.57
120 b = 3.43
b = 0.02861
x=1/a= 1/0.00227= 440 km/h-------------Train
y=1/b=1/0.02861= 35 km/h-------------- Car
CHECK
130/440 +140/35= 4.3 hours
m.ananth@hotmail.ca

Answer by MathTherapy(10552) About Me  (Show Source):
You can put this solution on YOUR website!
A man travels 370 KM partly by train and partly by car. If he covers 250 KM by train and the rest by car. it takes him 4 Hours. But if he travels 130 KM by train and rest by car. he taken 18 minut longer. Find the speed of the train and that of the car.

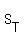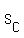Let the speed of train and car be S%5BT%5D and S%5BC%5D, respectively
Since he covered 250 km out of 370 km by train, then he travels 120 (370 – 250) km by car. Therefore, we have: 250%2FS%5BT%5D+%2B+120%2FS%5BC%5D+=+4, since the total journey took 4 hours
If he had covered 130 km out of 370 km by train, then he would’ve traveled 240 (370 – 130) km by car. Therefore, we have: 130%2FS%5BT%5D+%2B+240%2FS%5BC%5D+=+4.3, since the total journey took 18 mins more

We now have:

250%2FS%5BT%5D+%2B+120%2FS%5BC%5D+=+4 -------- eq (i)

130%2FS%5BT%5D+%2B+240%2FS%5BC%5D+=+4.3 -------- eq (ii)

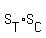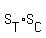250S%5BC%5D+%2B+120S%5BT%5D+=+4S%5BT%5D%2AS%5BC%5D ----- Multiplying eq (i) by LCD, S%5BT%5D+%2A+S%5BC%5D ------ eq (iii)

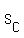
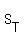130S%5BC%5D+%2B+240S%5BT%5D+=+4.3S%5BT%5D%2AS%5BC%5D ---- Multiplying eq (ii) by LCD, S%5BT%5D+%2A+S%5BC%5D --- eq (iv)

-+500S%5BC%5D+-+240S%5BT%5D+=+-+8S%5BT%5D%2AS%5BC%5D ------ Multiplying eq (iii) by – 2 ------- eq (v)

-+370S%5BC%5D+=+-+3.7S%5BT%5D%2AS%5BC%5D ------ Adding eqs (iv) & (v)

-+370+=+-+3.7S%5BT%5D+------ Factoring out S%5BC%5D

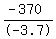S%5BT%5D, or speed of train = %28-+370%29%2F-+3.7, or highlight_green%28100%29 km/h

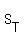%28250%2F100%29+%2B+120%2FS%5BC%5D+=+4 ------ Substituting 100 for S%5BT%5D in eq (i)
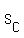2.5+%2B+120%2FS%5BC%5D+=+4
120%2FS%5BC%5D+=+4+-+2.5
120%2FS%5BC%5D+=+1.5
1.5S%5BC%5D+=+120 ----- Cross-multiplying

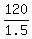S%5BC%5D, or speed of car = 120%2F1.5, or highlight_green%2880%29 km/h

-------
Check
-------

250%2FS%5BT%5D+%2B+120%2FS%5BC%5D+=+4
%28250%29%2F100+%2B+%28120%29%2F80+=+4

2.5 + 1.5 = 4
4 = 4 (TRUE)

130%2FS%5BT%5D+%2B+240%2FS%5BC%5D+=+4.3 -------- eq (ii)
%28130%29%2F100+%2B+%28240%29%2F80+=+4.3

1.3 + 3 = 4.3
4.3 = 4.3 (TRUE)

Send comments and “thank-yous” to “D” at MathMadEzy@aol.com