Question 53538: 1) Use the arithmetic sequence of numbers 1, 3, 5, 7, 9,…to find the following:
a) What is d, the difference between any 2 terms?
Answer:
Show work in this space.
b) Using the formula for the nth term of an arithmetic sequence, what is 101st term? Answer:
Show work in this space.
c) Using the formula for the sum of an arithmetic series, what is the sum of the first 20 terms?
Answer:
Show work in this space
d) Using the formula for the sum of an arithmetic series, what is the sum of the first 30 terms?
Answer:
Show work in this space
e) What observation can you make about these sums of this series (HINT: It would be beneficial to find a few more sums like the sum of the first 2, then the first 3, etc.)? Express your observations as a general formula in "n."
Answer:
Answer by funmath(2933)   (Show Source): (Show Source):
You can put this solution on YOUR website! 1) 1,3,5,7,9
a) d=a(sub n+1)-a(sub n)
d=3-1=2
d=5-3=2
d=7-5=2
d=9-7=2
d=2
-------------------------
b) a(sub n)= a(sub 1)+(n-1)d
n=101
d=2
a (sub 1)=1
a(sub 101)=1+(101-1)2
a(sub 101)=1+(100)2
a(sub 101)=1+200
a(sub 101)=201
--------------------------
c)

We need to find a(sub 20) to solve this:
a(sub 20)=1+(20-1)2
a(sub 20)=1+(19)2
a(sub 20)=1+38
a(sub 20)=39
n=20
a(sub 1)=1
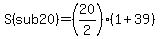

S(sub 20)=400
-----------------------------------
d)We need to use the formula we used above, but in order to use the formula, we have to find a(sub 30).
a(sub 30)=1+(30-1)2
a(sub 30)=1+(29)2
a(sub 30)=1+58
a(sub 30)=59


S(sub 30)=900
------------------------------------
e)You can use the methods above to find the first 6 S(sub n)'s.
S(sub 2)=4
S(sub 3)=9
S(sub 4)=16
S(sub 5)=25
S(sub 6)=36
Do you see the pattern? (for 2, 2^2=4),(for 3, 3^2=9), ect.
a(sub n)=1+(n-1)2
a(sub n)=1+2n-2
a(sub n)=-1+2n

I have a TI-83 and can tell you how to check yourself on a TI-83/84 if you have one. Let me know if you need the directions for that.
|
|
|