Question 534682: Consider a large bag of coins, consisting of only quarters ($0.25), dimes ($0.10), and nickels ($0.05). 40% of the coins are nickels, 35% are dimes, and 25% are quarters.
Randomly select 5 coins from the bag. What is the probability that your selection is worth at least $1.00? (Note that the only way to make $1 with 5 coins is with four (4) quarters and one (1) other coin.)
Answer by Edwin McCravy(20064)   (Show Source): (Show Source):
You can put this solution on YOUR website! Consider a large bag of coins, consisting of only quarters ($0.25), dimes ($0.10), and nickels ($0.05). 40% of the coins are nickels, 35% are dimes, and 25% are quarters.
You must draw either 5 quarters of 4 quarters and a nickel or dime.
Suppose there are 100N coins consisting of 40N nickels, 35N dimes, and 25N
quarters. Note: there are 75N non-quarters
The number of successes equals
the number of ways to draw 5 quarters is C(25N,5)
plus
the number of ways to draw 4 quarters and 1 non-quarter is C(25N,4)·(75N)
So the number of successes is
C(25N,5) + C(25N,4)·(75N)
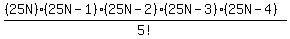 + + 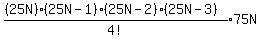 Put the (75N) in the numerator of the second fraction
Put the (75N) in the numerator of the second fraction
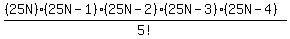 + + 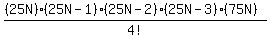 We get a least common denominator of 5! by multiplying the second fraction
by
We get a least common denominator of 5! by multiplying the second fraction
by 
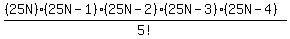 + + 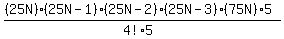
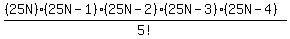 + + 
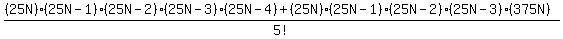 Factor the numerator:
Factor the numerator:
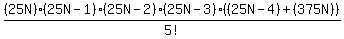

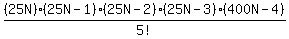 The number of possible ways is the number of ways to select any
5 coins from the 100N coins:
C(100N,5) =
The number of possible ways is the number of ways to select any
5 coins from the 100N coins:
C(100N,5) = 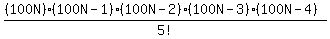 So the probability is
So the probability is
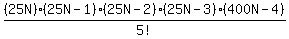 ÷ ÷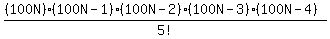
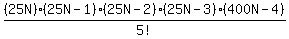 × ×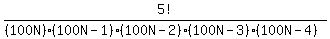
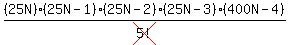 × ×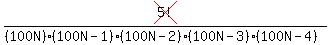

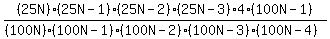
 The first fraction is
The first fraction is  , exactly , exactly  .
If N is large the next three are also very nearly .
If N is large the next three are also very nearly  or
or  , and the last fraction is very nearly , and the last fraction is very nearly 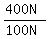 , or 4.
So that is very nearly , or 4.
So that is very nearly
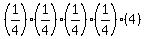
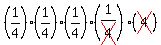
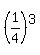
 That's not exact, but it is very close if N is large.
Edwin
That's not exact, but it is very close if N is large.
Edwin
|
|
|