|
Question 534552: What is the equation of the line that has a slope of -2 and passes through the point (1, 5)
Found 2 solutions by Earlsdon, KMST:
Answer by Earlsdon(6294)   (Show Source): (Show Source):
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! There are many ways to write an equation for the same line.
A popular one is the one that starts with "y = " It is called the slope-intercept form and looks like
 with m being a number called the slope and b being a number called the y-intercept or simply intercept. with m being a number called the slope and b being a number called the y-intercept or simply intercept.
The slope is the change in the y value divided by the corresponding change in the x value. So in a straight line with slope -2, the changes going from point (1,5) to a point (x,y), are
 for the change in x values, and for the change in x values, and
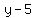 for the change in y values, with for the change in y values, with

From that, we get

That is the equation in what's called the point-slope form. You see the slope to the right of the equal sign, multiplying something in parenthesis. You see the x coordinate of the point known subtracted from x in that parenthesis. And you see the y coordinate of the point known, subtracted form y, on the left hand side.
We can go from the point-slope form above to any other form of the equation with a little algebra.
 as the first step (distributive property), and then as the first step (distributive property), and then
 adding 5 to both sides, takes us to the slope-intercept form. adding 5 to both sides, takes us to the slope-intercept form.
(I like the slope-intercept form because two equations for the same line in the slope-intercept form will always be identical, but you cannot say the same for the other forms. However, sometimes a problem specifies what form of the equation is desired, and it is good to follow instructions).
|
|
|
| |