Question 534356: a runner starts jogging at her house. She jogs 6 miles and then turns around and jogs back to her house. The first part of her job is mostly uphill, so her speed averages 3 miles per hour less than her returning spped. If the total time she spends jogging is 1 3/4 hours, find her speed going and her speed returning
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! a runner starts jogging at her house. She jogs 6 miles and then turns around and jogs back to her house. The first part of her job is mostly uphill, so her speed averages 3 miles per hour less than her returning speed. If the total time she spends jogging is 1 3/4 hours, find her speed going and her speed returning
:
let s = the uphill speed
then
(s+3) = the downhill speed
:
Change time to 1.75 hrs
:
Write a time equation, time = dist/speed
:
Up time + down time = total time
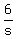 + + 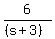 = 1.75 = 1.75
multiply by s(s+3) to clear the denominators, results:
6(s+3) + 6s = 1.75s(s+3)
6s + 18 + 6s = 1.75s^2 + 5.25s
Combine like terms
0 = 1.75s + 5.25s - 12s - 18
1.75s - 6.75s - 18 = 0
Use the quadratic formula to find s

x = s; a=1.75, b=-6.75, c=-18

You can do the rather tedious math here, you should get a positive solution
s = 5.67 mph, the speed uphill, and obviously, 8.67 mph down
|
|
|