Question 532499: This problem is from chapter 5.6 - Models Involving Rational Expressions - of the Intermediate Algebra textbook, 2nd Ed, Sullivan/Struve:
"Roger can run one mile in 8 minutes. Jeff can run one mile in 6 minutes. If Jeff gives Roger a 1-minute head start, how long will it take before Jeff catches up to Roger? How far will each have to run?"
I'm not sure what to do with this problem because there is no specific distance given. Can you please help me figure out the model for this problem?
Thank you for your help.
Answer by jkrsmsc76(5)   (Show Source): (Show Source):
You can put this solution on YOUR website! I'm looking at this from my way, which may not be the way you were taught, so I hope you can follow.
I'm going to be using the formula  for this, and modifying it as needed. for this, and modifying it as needed.
First, their rates 
Roger's Rate: 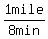 and Jeff's Rate: and Jeff's Rate: 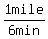
Now, their times for this race  We don't know the distance, so for Roger: We don't know the distance, so for Roger:  . For Jeff, it's a little more complicated, because we have to add on that extra 1 min: . For Jeff, it's a little more complicated, because we have to add on that extra 1 min: 
Both of these formulas can be simplified because we have fractions in fractions to get:
Roger:  and Jeff: and Jeff: 
The same amount of time will have elapsed when Jeff catches Roger, so set the 2 equations equal to each other, and solve for the distance.
Another way to do this is to graph both of their movements, having time be one axis and distance be the other. You will be able to see where the two intersect.
|
|
|