SOLUTION: 16y^2-9x^2+18x+64y-89=0

Algebra ->  Quadratic-relations-and-conic-sections -> SOLUTION: 16y^2-9x^2+18x+64y-89=0      Log On


   

Question 532249: 16y^2-9x^2+18x+64y-89=0
Answer by Edwin McCravy(20056) About Me  (Show Source):
You can put this solution on YOUR website!
16y² - 9x² + 18x + 64y - 89 = 0

That's a hyberbola because it has both x² and y² terms with opposite
signs when on the same side of the equation:

We have to get it to looking like this which opens upward and downward:

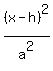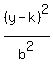      %28x+-+h%29%5E2%2Fa%5E2 - %28y+-+k%29%5E2%2Fb%5E2 = 1 

or this, which opens downward or upward:

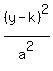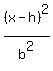      %28y+-+k%29%5E2%2Fa%5E2 - %28x+-+h%29%5E2%2Fb%5E2 = 1

        16y² - 9x² + 18x + 64y - 89 = 0

Get they y terms and the x terms together and the 
constant on the right:

             16y² + 64y - 9x² + 18x = 89

Factor the coefficient of y², which is 16, out of the first two terms.
Factor the coefficient of x², which is -9, out of the next two terms.

           16(y² + 4y) - 9(x² - 2x) = 89

Multiply the coefficient of y, which is 4, by 1%2F2, getting 2.
Then square 2, getting +4, add +4 inside the first parentheses which
is multiplied by 16 which amounts to multiplying 16·4, so we add
16·4 to the right side:

Multiply the coefficient of x, which is -2, by 1%2F2, getting -1.
Then square -1, getting +1, add +1 inside the second parentheses which
is multiplied by -9 which amounts to multiplying -9·1, so we add
-9·1 to the right side:

   16(y² + 4y + 4) - 9(x² - 2x + 1) = 89 + 16·4 - 9·1

Factor the trinomials in the parentheses and do some work on the right
side.

 16(y + 2)(y + 2) - 9(x - 1)(x - 1) = 89 + 64 - 9

Write the factorizations as the square of binomials and finish the 
right side:

             16(y + 2)² - 9(x - 1)² = 144

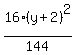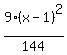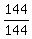
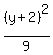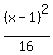                    16%28y+%2B+2%29%5E2%2F144 - 9%28x+-+1%29%5E2%2F144 = 144%2F144

                       %28y+%2B+2%29%5E2%2F9 - %28x+-+1%29%5E2%2F16 = 1 

This compares to:

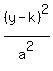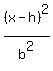                       %28y+-+k%29%5E2%2Fa%5E2 - %28x+-+h%29%5E2%2Fb%5E2 = 1

So it opens upward and downward.


            h = 1,  k = -2, a² = 9, so a = 3.  b² = 16, so b = 4.

The center is (h,k) = (1,-2).   

a = 3, so the transverse axis is 2·a or 6

b = 4, so the conjugate axis is 2·b or 8.

We draw the transverse axis vertically and the conjugate axis
horizontally, perpendicularly bisecting each other at the center (1,-2)

 

Draw the defining rectangle around that cross, which is the rectangle
with horizontal and vertical sides with the ends of the transverse and
vertical axes bisecting the sides:



Draw and extend the diagonals of that rectangle:



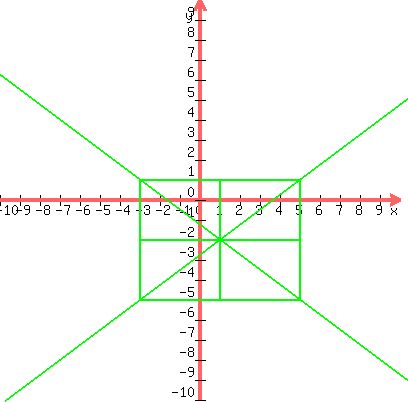Sketch in the hyperbola:


The equations of the asymptotes can be found use point-slope form:

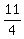y = 3%2F4x - 11%2F4

and

y = -3%2F4x - 5%2F4

The foci (or focal points) are c units on each side of the center
inside the two branches of the hyperbola, where

c² = a² + b²

c² = 3² + 4²

c² = 9 + 16

c² = 25

c = 5 

So they are 5 units above and below the center and are the
two points inside the two branches (1,-7) and (1,3).



Edwin