SOLUTION: How many distinguishable arrangements are there of the letters in "arrangement" that do not have the two "r"s adjacent?

First we must calculate the number of distinguishable arrangements
whether the R's come together or not, and then we must calculate the
number of arrangements when they come together, and then subtract
the second number from the first.

If it were 

ARraNGEMenTS, (where you could tell A from a, R from r, and N from n,
and E from e, the number of arrangements would be 12!

But since we cannot tell the difference between A and a, since they are both
capital, we have to divide by 2! so as not to count, say, these two,

AaEeGMNnRrST and aAEeGMNnRrST

as two separate arrangements.

So we take out what we consider as A-duplications and we get 
as the number of arrangements of AAEeGMNnRrST.
---
Also since we cannot tell the difference between E and e, since they are both
capital, we have to divide by 2! again so as not to count, say, these two,
AAEeGMNnRrST and AAeEGMNnRrST

as two separate arrangements.

So we take out what we consider as E-duplications and we get 
as the number of arrangements of AAEEGMNnRrST.
---
Also since we cannot tell the difference between N and n, since they are both
capital, we have to divide by 2! again so as not to count, say, these two,
AAEEGMNnRrST and AAEEGMnNRrST

as two separate arrangements.

So we take out what we consider as N-duplications and we get 
as the number of arrangements of AAEEGMNNRrST.
---
Also since we cannot tell the difference between R and r, since they are both
capital, we have to divide by 2! again so as not to count, say, these two,
AAEEGMNNRrST and AAEEGMNNrRST

as two separate arrangements.

So we take out what we consider as R-duplications and we get  
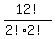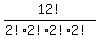as the number of arrangements of AAEEGMNNRRST.  

That's  =  = 29937600  

-----

Now we must calculate the number of arrangements where the R's come together,
so we can subtract them from the above number.

If the R's come together, we are finding the number of arrangements
 of the 11 things A[RR]ANGEMENTS, where the [RR] is considered as
if it were one single letter instead of two letters.

--------- 

Similar to the first, if it were 

A[RR]aNGEMenTS, (where you could tell A from a, R from r, and N from n,
and E from e, the number of arrangements would be 11!

But since we cannot tell the difference between A and a, since they are both
capital, we have to divide by 2! so as not to count, say, these two,

AaEeGMNn[RR]ST and aAEeGMNn[RR]ST

as two separate arrangements.

So we take out what we consider as A-duplications and we get 
as the number of arrangements of AAEeGMNnRRST.
---
Also since we cannot tell the difference between E and e, since they are both
capital, we have to divide by 2! again so as not to count, say, these two,
AAEeGMNn[RR]ST and AAeEGMNn[RR]ST

as two separate arrangements.

So we take out what we consider as E-duplications and we get 
as the number of arrangements of AAEEGMNn[RR]ST.
---
Also since we cannot tell the difference between N and n, since they are both
capital, we have to divide by 2! again so as not to count, say, these two,
AAEEGMNn[RR]ST and AAEEGMnN[RR]ST

as two separate arrangements.

So we take out what we consider as N-duplications and we get 
as the number of arrangements of AAEEGMNN[RR]ST.
  

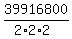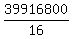That's  =  = 4989600

--------------------

So we subtract to get the final answer:

29937600 - 4989600 = 2948000

And that's the number of distinguishable arrangements of ARRANGEMENTS
where the two R's are not together.
 
Edwin