In Paul's bank,there is $2.60 in pennies, nickles,and dimes. In all there are 45 coins. If there are twice as many nickles as pennies, find how many of each kind there are if you only use one variable.
let p = the number of pennies
>>...there are twice as many nickles as pennies...<<
then 2p = the number of nickels
>>...there are 45 coins...<<
 = 45 -
= 45 -  -
- 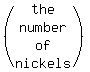 So the number of dimes = 45 - p - 2p = 45 - 3p
So the number of dimes = 45 - p - 2p = 45 - 3p
>>...there is $2.60...<<
$0.01 + $0.05
+ $0.05 + $0.10
+ $0.10 = $2.60
$0.01(p) + $0.05(2p) + $0.10(45 - 3p) = $2.60
Multiply through by 100 and drop the dollar marks:
1(p) + 5(2p) + 10(45 - 3p) = 260
p + 10p + 450 - 30p = 260
-19p + 450 = 260
-19p = -190
p = 10
So the number of pennies = p = 10
the number of nickels = 2p = 2(10) = 20
the number of dimes = 45 - 3p = 45 - 3(10) = 45 - 30 = 15
We used only one variable, p.
Edwin
= $2.60
$0.01(p) + $0.05(2p) + $0.10(45 - 3p) = $2.60
Multiply through by 100 and drop the dollar marks:
1(p) + 5(2p) + 10(45 - 3p) = 260
p + 10p + 450 - 30p = 260
-19p + 450 = 260
-19p = -190
p = 10
So the number of pennies = p = 10
the number of nickels = 2p = 2(10) = 20
the number of dimes = 45 - 3p = 45 - 3(10) = 45 - 30 = 15
We used only one variable, p.
Edwin