SOLUTION: How many different 10-letter words (real or imaginary) can be formed from the following letters? IMWOSWMCIA

Algebra ->  Permutations -> SOLUTION: How many different 10-letter words (real or imaginary) can be formed from the following letters? IMWOSWMCIA      Log On


   

Question 530844: How many different 10-letter words (real or imaginary) can be formed from the following letters? IMWOSWMCIA
Answer by Edwin McCravy(20054) About Me  (Show Source):
You can put this solution on YOUR website!
If it were 

IMWOSwmCiA, (where you could tell I from i, M from m, and W from w 

it would be 10!

But since we cannot tell the difference between i and I, since they are both
capital, we have to divide by 2! so as not to count iMWOSwmCIA and IMWOSwmCiA
as two separate arrangements.

So we take out what we consider as I-duplications and we get 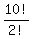10%21%2F2%21
as the number of arrangements of IMWOSwmCIA.

But since we also cannot tell the difference between m and M, we have to 
divide by 2! again so as not to count ImWOSwMCIA and IMWOSwmCIA as two 
separate arrangements.

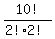So we take out what we consider as M-duplications and we get 10%21%2F%282%212%21%29
as the number of arrangements of IMWOSwMCIA.

But since we also cannot tell the difference between w and W, we have to
divide by 2! again so as not to count IMwOSWMCIA and IMWOSwMCIA as two separate
arrangements.

So we take out what we consider as W-duplications and finally we get
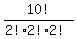10%21%2F%282%212%212%21%29 as the number of arrangements of IMWOSWMCIA.


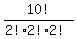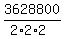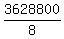10%21%2F%282%212%212%21%29 = 3628800%2F%282%2A2%2A2%29 = 3628800%2F8 = 453600.

And that's the number of distinguishable arrangements of IMWOSWMCIA.
 
Edwin