You can
put this solution on YOUR website!
Start with this:
__________________
-3x²-5x-2)-9x³-18x²-11x - 2
Divide 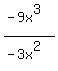 getting 3x
write 3x above the top line:
3x
-3x²-5x-2)-9x³-18x²-11x - 2
Next multiply 3x by -3x²-5x-2, 3x(-3x²-5x-2), getting -9x³-15x-6x
and write this below and underline it like this:
3x
-3x²-5x-2)-9x³-18x²-11x - 2
-9x³-15x²- 6x
Next subtract (-9x³-18x²-11x)-(-9x³-15x²- 6x) =
-9x³-18x²-11x+9x³+15x²+6x = -3x²-5x
and write that below the line:
3x
-3x²-5x-2)-9x³-18x²-11x - 2
-9x³-15x²- 6x
-3x²- 5x
Bring down the -2
3x
-3x²-5x-2)-9x³-18x²-11x - 2
-9x³-15x²- 6x
-3x²- 5x - 2
Divide
getting 3x
write 3x above the top line:
3x
-3x²-5x-2)-9x³-18x²-11x - 2
Next multiply 3x by -3x²-5x-2, 3x(-3x²-5x-2), getting -9x³-15x-6x
and write this below and underline it like this:
3x
-3x²-5x-2)-9x³-18x²-11x - 2
-9x³-15x²- 6x
Next subtract (-9x³-18x²-11x)-(-9x³-15x²- 6x) =
-9x³-18x²-11x+9x³+15x²+6x = -3x²-5x
and write that below the line:
3x
-3x²-5x-2)-9x³-18x²-11x - 2
-9x³-15x²- 6x
-3x²- 5x
Bring down the -2
3x
-3x²-5x-2)-9x³-18x²-11x - 2
-9x³-15x²- 6x
-3x²- 5x - 2
Divide 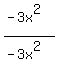 getting +1
write +1 above the top line:
3x + 1
-3x²-5x-2)-9x³-18x²-11x - 2
-9x³-15x²- 6x
-3x²- 5x - 2
Next multiply 1 by -3x²-5x-2, 1(-3x²-5x-2), getting -3x²-5x-2
and write this below and underline it like this:
3x + 1
-3x²-5x-2)-9x³-18x²-11x - 2
-9x³-15x²- 6x
-3x²- 5x - 2
-3x²- 5x - 2
Next subtract (-3x²-5x-2)-(-3x²-5x-2) =
-3x²-5x-2+3x²+5x+2 = 0
We write this 0 remainder down at the bottom
3x + 1
-3x²-5x-2)-9x³-18x²-11x - 2
-9x³-15x²- 6x
-3x²- 5x - 2
-3x²- 5x - 2
0
And that's it. The answer is 3x + 1 with 0 remainder.
Edwin
getting +1
write +1 above the top line:
3x + 1
-3x²-5x-2)-9x³-18x²-11x - 2
-9x³-15x²- 6x
-3x²- 5x - 2
Next multiply 1 by -3x²-5x-2, 1(-3x²-5x-2), getting -3x²-5x-2
and write this below and underline it like this:
3x + 1
-3x²-5x-2)-9x³-18x²-11x - 2
-9x³-15x²- 6x
-3x²- 5x - 2
-3x²- 5x - 2
Next subtract (-3x²-5x-2)-(-3x²-5x-2) =
-3x²-5x-2+3x²+5x+2 = 0
We write this 0 remainder down at the bottom
3x + 1
-3x²-5x-2)-9x³-18x²-11x - 2
-9x³-15x²- 6x
-3x²- 5x - 2
-3x²- 5x - 2
0
And that's it. The answer is 3x + 1 with 0 remainder.
Edwin