SOLUTION: what is the equation of the function for a parabola that moves 3 units to the left of the origin,8 units down from the origin, is flipped over the x-axis, and is stretched vertical

Algebra ->  Expressions-with-variables -> SOLUTION: what is the equation of the function for a parabola that moves 3 units to the left of the origin,8 units down from the origin, is flipped over the x-axis, and is stretched vertical      Log On


   

Question 530003: what is the equation of the function for a parabola that moves 3 units to the left of the origin,8 units down from the origin, is flipped over the x-axis, and is stretched vertically five times as much as the basic f(x)=x^2
Answer by Edwin McCravy(20055) About Me  (Show Source):
You can put this solution on YOUR website!
what is the equation of the function for a parabola that moves 3 units to the left of the origin,8 units down from the origin, is flipped over the x-axis, and is stretched vertically five times as much as the basic f(x)=x^2
We start with the basic 

f(x) = x², which has this red graph:

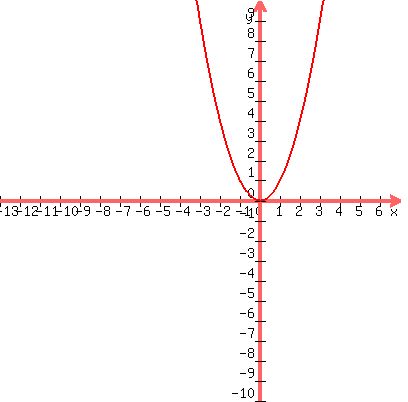graph%28400%2C400%2C-13%2C7%2C-10%2C10%2C+x%5E2%29

Then we move the red graph of f(x) 3 units left, 
by replacing x by (x+3) and getting

g(x) = (x+3)², which has this green graph:

graph%28400%2C400%2C-13%2C7%2C-10%2C10%2C+x%5E2%2C+%28x%2B3%29%5E2%29

 
Then we move the green graph of g(x) 8 units down, 
by subtracting 8 from the right side of g(x), getting

h(x) = (x+3)²-9, which has this blue graph:

graph%28400%2C400%2C-13%2C7%2C-10%2C10%2C+20%2C+%28x%2B3%29%5E2%2C+%28x%2B3%29%5E2-9%29

Then we flip the blue graph of h(x) over the x-axis, 
by multiplying the right side of h(x) by -1, getting

i(x) = -(x+3)²+9, which has this purplish lavender graph:



Finally we stretch the purplish lavender graph of i(x) vertically by a 
factor of 5, by multiplying the right side of i(x) by 5, 
getting

j(x) = -5(x+3)²+45, which has this long light yellow-green-grayish graph:




Edwin