SOLUTION: three fourths of a number increased by 32 is no more than 58. i cant figure it out please get back to me before 3:30

Algebra ->  Inequalities -> SOLUTION: three fourths of a number increased by 32 is no more than 58. i cant figure it out please get back to me before 3:30       Log On


   

Question 529979: three fourths of a number increased by 32 is no more than 58. i cant figure it out please get back to me before 3:30
Answer by KMST(5328) About Me  (Show Source):
You can put this solution on YOUR website!
I believe they mean that after figuring out three fourth the number, then you increase that by 32. That would be, following tradition by calling the mistery number x,
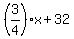
%283%2F4%29%2Ax%2B32
If it's no more than 58, then it's less than or equal to 58, so
%283%2F4%29%2Ax%2B32%3C=58
You do the same operations to both sides, carefully undoing what has been done to x.
First we subtract 32 (undoing the last thing done) to get
%283%2F4%29%2Ax%3C=58-32 or %283%2F4%29%2Ax%3C=26
Then we undo the three fourths calculation/multiplication by dividing by3%2F4, which means mutiplying by 4%2F3
to get
x%3C=26%2A%284%2F3%29 or x%3C=104%2F3 or x%3C=34%2B%282%2F3%29
CAUTION:
When multiplying/dividing both sides of an inequality by the same number, you have to be careful. If the number is negative, you have to flip < to > and viceversa. For example, it should be obvious that if
x%3C0 then multiplying both sides by -1
it makes sense to get -x%3E0.