Question 529116: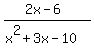 
What I have to do here is find the y-intercept, the zeros, domain, x-intercept, and end behavior.
I know that you have to simplify the factors, which would be
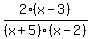
I just don't know what else to do to find the rest. I know that to find the y-intercept you have to set the x to zero, correct? And to find the x-intercept you set the whole equation to zero.
Answer by KMST(5328)   (Show Source):
You can put this solution on YOUR website! Your work is already half done.
You are correct about the y-intercept.
The factoring
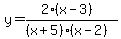
tells you a lot about the function.
Look at when each factor in parenthesis is zero.
It says that for   .
That's the x intercept, where the graph crosses the x-axis.
You also see from the factoring that the function changes sign each time one of those parentheses changes sign.
It is negative when all three parentheses are negative, for  .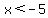
It becomes positive between -5 and 2.
It's negative again between 2 and 3,
and it's positive for  .
You also see that the function does not exist for
 and for 
because they make the denominator zero. Those values of x are not part of the domain of the function, but other than that, all other real numbers are in the domain.
As x approaches -5, the factor  aproaches zero, while the other factors are close to finite numbers. Very near -5, the function could be approximated by
 .
That means it goes down towards minus infinity on the left side of the vertical line x=5 and comes back down from plus infinity on the other side of -5.
Something similar, but reversed happens around x=2.
Both, x=-5 and x=2 are vertical asymptotes.
Even more can be said about the behavior of the function.
For very large x, and for very large -x, y is very small. The function hugs the x- axis as you go to one or the other extremes of x. The x- axis is an asymptote on both sides (a horizontal one).
Maybe you could see that better if you wrote it as
|
|
|
