Question 528387: If you roll two six-sided dice, what is the probability that at least one die shows a 1, 2, 3, or 4, or the sum is odd?
Answer by Edwin McCravy(20056)   (Show Source): (Show Source):
You can put this solution on YOUR website!
There are only 4 rolls that don't show 1,2,3, or 4.
They are (5,5), (5,6), (6,5) and (6,6) and two of those
have odd sums, so there are only 2 rolls (5,5) and (6,6)
which don't have at least one die showing a 1, 2, 3, or 4,
or the sum is odd, and those are (5,5) and (6,6). So the
other 34 rolls fit the category. So the probability is
34 out of the 36 or 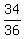 which reduces to which reduces to 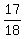 .
⚀⚀ ⚀⚁ ⚀⚂ ⚀⚃ ⚀⚄ ⚀⚅
⚁⚀ ⚁⚁ ⚁⚂ ⚁⚃ ⚁⚄ ⚁⚅
⚂⚀ ⚂⚁ ⚂⚂ ⚂⚃ ⚂⚄ ⚂⚅
⚃⚀ ⚃⚁ ⚃⚂ ⚃⚃ ⚃⚄ ⚃⚅
⚄⚀ ⚄⚁ ⚄⚂ ⚄⚃ ⚄⚄ ⚄⚅
⚅⚀ ⚅⚁ ⚅⚂ ⚅⚃ ⚅⚄ ⚅⚅
The 34 red ones out of the 36 rolls or .
⚀⚀ ⚀⚁ ⚀⚂ ⚀⚃ ⚀⚄ ⚀⚅
⚁⚀ ⚁⚁ ⚁⚂ ⚁⚃ ⚁⚄ ⚁⚅
⚂⚀ ⚂⚁ ⚂⚂ ⚂⚃ ⚂⚄ ⚂⚅
⚃⚀ ⚃⚁ ⚃⚂ ⚃⚃ ⚃⚄ ⚃⚅
⚄⚀ ⚄⚁ ⚄⚂ ⚄⚃ ⚄⚄ ⚄⚅
⚅⚀ ⚅⚁ ⚅⚂ ⚅⚃ ⚅⚄ ⚅⚅
The 34 red ones out of the 36 rolls or 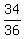 or or 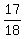 Edwin
Edwin
|
|
|