Question 52743This question is from textbook Algebra 1
: Ho w do i solve for t in this problem?:  This question is from textbook Algebra 1
This question is from textbook Algebra 1
Answer by whitetiger78(1)   (Show Source): (Show Source):
You can put this solution on YOUR website!  The first thing you must do when solving for any similar problem is to get all like expressions on the same side of the equal sign. The first thing you must do when solving for any similar problem is to get all like expressions on the same side of the equal sign.
Let's start by moving one of the expressions containing t to the opposite side of the equation.
I'll start by adding (t/4) to both sides.
 . .
Now simplify the right side remembering that 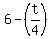 is the same as is the same as 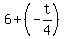 . So, . So, 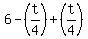 becomes becomes 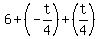 . .
Since both t expressions have the same denominator we can add the like terms. This gives us 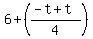 , and 0 divided by 4 is 0. , and 0 divided by 4 is 0.
So our equation now looks like this,  . .
Now, to have only the t expressions on the same side of the equation we will subtract 8 from both sides,  . .
Next, simplify each side to get  . .
Our next step will be to add the t expressions but first we must get a least common denominator.
Our least common denominator is 4 so we have to multiply (t/2) times 2, which means both the numerator and denominator or multiplied by 2  . .
Next, we add like terms  which equals which equals  . .
Now, multiply both sides by 4 to negate the denominator.
This will give us,  . .
Now we have  . .
Divide both sides by 3 and you have your answer,

|
|
|