|
Question 526825: 1) A large pipe and a small pipe are used to fill a tank and a third pipe is used to drain the tank. If the three pipes are open, it takes 3 hours to fill the tank. If the large pipe and the drain are open and the small pipe is closed, it takes 6 hours to fill the tank. If the small pipe and the drain are open and the large pipe is closed, it takes 12 hours to fill the tank. How long will it take each pipe to fill the tank alone if the drain is closed and how long will it take the drain to empty a full tank?
2) On a store counter, there was a supply of three sizes of Christmas cards. The large cards cost $25 each; the medium cards cost $20 each and the small cards cost $10 each. A woman purchased eighteen cards, which consisted of one fifth of the available large card, one third of the available medium cards and one fourth of the available small cards. The total cost of her cards was $295. If there were 50 cards remaining on the counter after her purchase, how many each kind of card did she buy?
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! 1) A large pipe and a small pipe are used to fill a tank and a third pipe is used to drain the tank.
If the three pipes are open, it takes 3 hours to fill the tank.
If the large pipe and the drain are open and the small pipe is closed, it takes 6 hours to fill the tank.
If the small pipe and the drain are open and the large pipe is closed, it takes 12 hours to fill the tank.
How long will it take each pipe to fill the tank alone if the drain is closed and how long will it take the drain to empty a full tank?
:
let a = the large pipe open
let b = small pipe open
let c = drain pipe open
let the completed job = 1, a full tank
:
Write an equation for each statement:
:
"1) If the three pipes are open, it takes 3 hours to fill the tank."
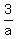 + + 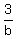 - - 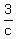 = 1 = 1
:
"If the large pipe and the drain are open and the small pipe is closed, it takes 6 hours to fill the tank."
 - - 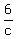 = 1 = 1
:
If the small pipe and the drain are open and the large pipe is closed, it takes 12 hours to fill the tank."
 - - 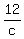 = 1 = 1
:
multiply the 1st equation by 2, subtract the 2nd equation
 + +  - - 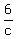 = 2 = 2
 + + 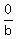 - - 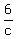 = 1 = 1
---------------------------------------Subtraction eliminates a and c, find b
 = 1 = 1
b = 6 hrs alone to fill the tank
Find c
 - - 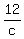 = 1 = 1
multiply by 6c, results
12c - 6(12) = 6c
12c - 72 = 6c
12c - 6c = 72
6c = 72
c = 72/6
c = 12 hrs to drain a full tank alone
:
Find a
 - - 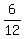 = 1 = 1
multiply by 12a, results
12(6) - 6a = 12a
72 - 6a = 12a
72 = 12a + 6a
72 = 18a
a = 72/18
a = 4 hrs to fill alone
:
Summarize: a=4 hrs to fill, b=6 hrs to fill, c=12 hrs to drain
:
Check solutions in the 1st equation
 + +  - - 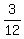 = =
 + + 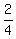 - -  = 4/4 = 1 = 4/4 = 1
:
:
2) On a store counter, there was a supply of three sizes of Christmas cards.
The large cards cost $25 each; the medium cards cost $20 each and the small cards cost $10 each.
A woman purchased eighteen cards, which consisted of one fifth of the available large card, one third of the available medium cards and one fourth of the available small cards.
The total cost of her cards was $295.
If there were 50 cards remaining on the counter after her purchase, how many each kind of card did she buy?
:
Let L = no. of large cards
Let M = no. of medium cards
Let s = no. of small ones
:
Write an equation for each statement:
:
"A woman purchased eighteen cards"
L + M + S = 18
:
" The total cost of her cards was $295."
25L + 20M + 10S = 295
:
"If there were 50 cards remaining on the counter after her purchase," Therefore:
18+50 = 68 card originally
:
"which consisted of one fifth of the available large card, one third of the available medium cards and one fourth of the available small cards."
therefore original total of the 3 kinds of cards will be
5L + 3M + 4S = 68
:
Multiply the 1st equation by 3, subtract from the above equation:
5L + 3M + 4S = 68
3L + 3M + 3s = 54
------------------Subtraction eliminates M:
2L + S = 14
:
Multiply the 1st equation by 20, subtract the cost equation
20L + 20M + 20S = 360
25L + 20M + 10S = 295
------------------------Subtraction eliminates M
-5L + 10S = 65
Simplify divide by 5
-L + 2S = 13
Multiply by 2, add
-2L + 4S = 26
+2L + S = 14
-------------- adding eliminates L, find S
0 + 5S = 40
S = 40/5
S = 8 small cards purchased
:
Find L
2L + S = 14
2L + 8 = 14
2L = 14-8
2L = 6
L = 3 large cards purchased
:
Find M
3 + M + 8 = 18
M = 18-11
M = 7 Medium cards purchased
:
:
Check this in the cost equation
25(3) = 20(7) + 10(8) =
75 + 140 + 80 = 295
|
|
|
| |