|
Question 526783: sammy can mow a lawn in 3 hours. his two young brothers can each do the job in 2 hours. if sammy and his two young brothers work together, how long would it take them to mow a lawn?
Answer by KMST(5328)   (Show Source): (Show Source):
You can put this solution on YOUR website! The trick for rate of work problems is to think in terms of rates, or ratios, which are fractions. Someone thought of solving the problem that way once, and the rest of us, the uninspired, who had been scratching our heads raw trying to figure it out, took note of it, and will remember it forever.
Do not be afraid of fractions. The question is how fast each person can work. It can be expressed as a rate of work, maybe in units of lawns per hour.
How many lawns can Sammy mow in one hour?

How many lawns can his two young brothers mow in one hour?

How many lawns will be mowed in an hour if all of them are working?

Now, to find the time necessary to do the work you need to multiply or divide by the right ratio (fraction).
The ratios you have for the 3 brothers working together are
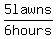 and and 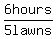
You get the same answer if you divide, like this:
 / /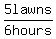
or multiply, like this:

Many teachers are particular about how you show your work, so you will have to figure out that by yourself.
|
|
|
| |