|
Question 526175: Jane's employer gave her a bonus of $1600. She decided to invest all the money, some at 5%, some at 7%, and some at 8%. She invested three times more money at 8% than she did at 5%. At the end of one year the total interest she earned was $115.
a) solve the problem
b) If you did not know that jane invested three times more money at 8% than she did at 5%, could you still solve the problem? Why or Why not?
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! Jane's employer gave her a bonus of $1600.
She decided to invest all the money, some at 5%, some at 7%, and some at 8%.
She invested three times more money at 8% than she did at 5%.
At the end of one year the total interest she earned was $115.
:
a) Solve the problem
Let a = amt invested at 5%
Let b = amt invested at 7%
Let c = amt invested at 8%
:
total amt invested
a + b + c = 1600
:
total interest equation
.05a + .07b + .08c = 115
:
Equation for the statement:
"She invested three times more money at 8% than she did at 5%."
c = 3a
:
Replace c with 3a in the amt invested and the interest equation
a + b + 3a = 1600
4a + b = 1600
arrange for substitution
b = (-4a + 1600)
and the interest equation
.05a + .07b + .08(3a) = 115
.05a + .07b + .24a = 115
.29a + .07b = 115
Replace b with (-4a+1600), find a
.29a + .07(-4a+1600) = 115
.29a - .28a + 112 = 115
.01a = 115 - 112
.01a = 3
a = 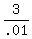
a = $300 invested at 5%
then
b = -4(300) + 1600
b = -1200 + 1600
b = $400 invested at 7%
:
and we know c = 3a, therefore
c = 3(300)
c = $900 invested at 8%
:
Check solutions in the interest equation
.05(300) + .07(400) + .08(900) = 0
15 + 28 + 72 = 115
b) If you did not know that jane invested three times more money at 8% than she did at 5%, could you still solve the problem? Why or Why not?
:
No. Generally you need the same number of equations as there are unknowns
If you did not know a = 3c, you would have only two equations, and three unknowns
|
|
|
| |