Question 525096: At the airport, Cheryl and Bill are walking to the gate (at the same speed) to catch their flight to Las Vegas. Since Bill wants a window seat, he steps onto the moving sidewalk and continues to walk while Cheryl uses the stationary walkway. If the sidewalk moves at 1 mps and Bill saves 50 seconds covering the 300-meter distance, what is their walking speed.
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! At the airport, Cheryl and Bill are walking to the gate (at the same speed) to catch their flight to Las Vegas.
Since Bill wants a window seat, he steps onto the moving sidewalk and continues to walk while Cheryl uses the stationary walkway.
If the sidewalk moves at 1 mps and Bill saves 50 seconds covering the 300-meter distance, what is their walking speed.
:
Let w = normal walking speed mps
then
(w+1) = speed on the moving walkway
:
Write a time equation; time = dist/speed
:
normal time - walkway time = 50 sec
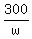 - -  = 50 = 50
multiply by w(w+1), results
300(w+1) - 300w = 50w(w+1)
300w + 300 - 300w = 50w^2 + 50w
A quadratic equation
0 = 50w^2 + 50w - 300
simplify, divide by 50
w^2 + w - 6 = 0
Factors to
(w+3)(w-2) = 0
the positive solution
w = 2 mps, normal walking speed
:
:
Check this by finding the actual time of each walker
300/2 = 150 sec
300/3 = 100 sec
---------------
differ: 50 sec, confirms our solution
|
|
|