Question 522446: The mean of 5 numbers, two of which are equal, is 8. When the two equal numbers are removed, the mean of the remaining three numbers is also 8. what numbers were removed?
Here is how I started the problem"
(a+b+c+d+e) / 5 = 8 We know d=e d=? e= ?
so multiply both sides by 5 and you get a+b+c+d+e=40 and a+b+c=24 so d+e=14 so they are both 7 d=7 e=7
(a+b+c) / 3 = 8
I can't check my work though, so I have no idea if I am right.
Found 2 solutions by Edwin McCravy, scott8148:
Answer by Edwin McCravy(20064)   (Show Source): (Show Source):
You can put this solution on YOUR website!
No, it's 8.
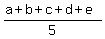 = 8
Multiply both sides by 5
a+b+c+d+e = 40
e = d
Substituting
a+b+c+d+d = 40
a+b+c+2d = 40
---------------- = 8
Multiply both sides by 5
a+b+c+d+e = 40
e = d
Substituting
a+b+c+d+d = 40
a+b+c+2d = 40
----------------
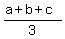 = 8
Multiply both sides by 3
a+b+c = 24
Multiply by -1
-a-b-c = -24
Add equals to equals:
a+b+c+2d = 40
-a-b-c = -24
---------------
0+0+0+2d = 16
2d = 16
d = 8
Answer: So the two 8's were removed.
There are many. many examples of such sets of 5 numbers but
in every case there are 2 8's that are removed.
One case is this
a=4, b=9, c=11, d=8, e=8
Another case is
a=5, b=7, c=12, d=8, e=8
Just make sure that a+b+c = 24
It may be stretching it a bit,
but perhaps one case could even be
a=8, b=8, c=8, d=8, e=8
because it didn't say more than two couldn't also be equal.
But anyway, the answer must be 8.
Edwin = 8
Multiply both sides by 3
a+b+c = 24
Multiply by -1
-a-b-c = -24
Add equals to equals:
a+b+c+2d = 40
-a-b-c = -24
---------------
0+0+0+2d = 16
2d = 16
d = 8
Answer: So the two 8's were removed.
There are many. many examples of such sets of 5 numbers but
in every case there are 2 8's that are removed.
One case is this
a=4, b=9, c=11, d=8, e=8
Another case is
a=5, b=7, c=12, d=8, e=8
Just make sure that a+b+c = 24
It may be stretching it a bit,
but perhaps one case could even be
a=8, b=8, c=8, d=8, e=8
because it didn't say more than two couldn't also be equal.
But anyway, the answer must be 8.
Edwin
Answer by scott8148(6628)   (Show Source): (Show Source):
You can put this solution on YOUR website! try this
"The mean of 5 numbers, two of which are equal, is 8" ___ a + b + c + d + d = 5 * 8
"When the two equal numbers are removed, the mean of the remaining three numbers is also 8" ___ a + b + c = 3 * 8
subtracting the equations ___ d + d = 2 * 8
|
|
|