Question 522222: Please help! I would really appreciate it.
I have to write these equations in vertex form and tell whether they open up or down.
1.The vertex of the parabola is the (2,5)Point T (3,0) lies on the graph of the parabola.
2.The vertex of the parabola is the (-3,-5. Point G (1,6) lies on the graph of the parabola)
Answer by Edwin McCravy(20056)   (Show Source):
You can put this solution on YOUR website! 1. The vertex of the parabola is the (2,5)Point T (3,0) lies on the graph of the parabola.
We plot the vertex (2,5) and the point T(3,0).
Next we plot the line (axis) of symmetry, which is the vertical line
that goes through the vertex, the green line below:
On the other side (left side) of the green line of symmetry, plot
the point that is just as far to the left of the green line and on
the same level as T(3,0), which is this one:
We can sketch in the graph as this:
We see that the parabola opens downward, and therefore we suspect
that "a" is a negative number.
The equation of the parabola is of the form
y = a(x-h)² + k
where the vertex is (h,k), so (h,k) = (2,5), so we substitute h=2 and k=5.
y = a(x-2)²+5
Now all we lack is the value of "a".
Since the parabola contains the point T(3,0) we can substitute
x=3, y=0, and the equation will be true, so:
0 = a(3-2)²+5
0 = a(1)² + 5
0 = a + 5
-5 = a
Substituting -5 for a, the equation of the parabola
y = a(x-2)²+5
is now complete as
y = -5(x-2)²+5
------------------------------
2. The vertex of the parabola is the (-3,-5). Point G(1,6) lies on the graph of the parabola)
We plot the vertex (-3,-5) and the point G(1,6).
Next we plot the line (axis) of symmetry, which is the vertical line
that goes through the vertex, the green line below:
On the other side (left side) of the green line of symmetry, plot
the point that is just as far to the left of the green line and on
the same level as G(1,6), which is this one:
We can sketch in the graph as this parabola:
We see that the parabola opens upward, and therefore we suspect
that "a" is a positive number.
The equation of the parabola is of the form
y = a(x-h)² + k
where the vertex is (h,k), so (h,k) = (-3,-5), so we substitute h=-3 and k=-5.
y = a(x-(-3))²+(-5)
y = a(x+3)²-5
Now all we lack is the value of "a".
Since the parabola contains the point G(1,6) we can substitute
x=1, y=6, and the equation will be true, so:
6 = a(1+3)²-5
6 = a(4)² - 5
6 = 16a - 5
11 = 16a
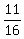 = a
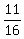Substituting for a, the equation of the parabola
y =  (x+3)²-5
Edwin
|
|
|
