Following clues describe a list of 5 integers. What is the greatest of the number in the list?
clue 1-two of the numbers are negative
clue 2-the median value is 8, the mean is 18.6 and the range is 60
clue 3-one of the numbers is a perfect square, andone of the numbers is one more than a perfect square
clue 4-the difference between the least two integers is 6
I'm stuck
Let the five numbers be A,B,C,D,E where A ≦ B ≦ C ≦ D ≦ E.
clue 2-the median value is 8,
For a set of 5 numbers (or any odd number of numbers),
the median is the middle number when they are listed
smallest to largest.
so we have C = 8, and we now have:
A ≦ B ≦ 8 ≦ D ≦ E
clue 1-two of the numbers are negative
Those have to be A and B. So we can insert 0 in between the B and the 8.
A ≦ B < 0 < 8 ≦ D ≦ E
clue 4-the difference between the least two integers is 6
The two negative ones have to be the least two, which are A and B.
That means B - A = 6 or
(1) B = A+6,
so replacing B by A+6 we have:
A < A+6 < 0 < 8 ≦ D ≦ E
...the mean is 18.6
So we add them up, divide by 5 and that must equal 18.6:
 Multiply through by 5 to clear of fractions.
2A+14+D+E = 18.6×5 =
Simplify:
2A+14+D+E = 93
(2) 2A+D+E = 79
and the range is 60, so
E-A = 60, or
(3) E-60 = A
Use (3) to substitute E-60 for A in (2)
(2) 2A+D+E = 79
2(E-60)+D+E = 79
2E-120+D+E = 79
3E+D = 199
(4) D = 199-3E
We know that D must be 8 or larger, so
D ≧ 8
Use (4) to substitute 199-3E for D
199-3E ≧ 8
Solve for E
-3E ≧ -191
Dividing through by a negative number, -3, reverses the inequality:
E ≦
Multiply through by 5 to clear of fractions.
2A+14+D+E = 18.6×5 =
Simplify:
2A+14+D+E = 93
(2) 2A+D+E = 79
and the range is 60, so
E-A = 60, or
(3) E-60 = A
Use (3) to substitute E-60 for A in (2)
(2) 2A+D+E = 79
2(E-60)+D+E = 79
2E-120+D+E = 79
3E+D = 199
(4) D = 199-3E
We know that D must be 8 or larger, so
D ≧ 8
Use (4) to substitute 199-3E for D
199-3E ≧ 8
Solve for E
-3E ≧ -191
Dividing through by a negative number, -3, reverses the inequality:
E ≦ 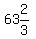
Clue 3-one of the numbers is a perfect square, andone of the numbers is one more than a perfect square
So one of D and E is a perfect square and the other is one more than
a perfect square. So we try perfect squares and 1 more than perfect
squares less than 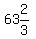 and larger than 8, for D and E.
perfect squares: 9, 16, 25, 36, 49
perfect squares plus1: 10, 17, 26, 37, 50
Let's try D = 49 in (4)
D = 199-3E
49 = 199-3E
3E = 150
E = 50
and E=50 is one of those "perfect square + 1's, namely 1 more than 49, or D.
So I think we have it.
Substitute D = 49 and E = 50 in (2)
(2) E-60 = A
50-60 = A
-10 = A
and substituting in (1)
B = A+6
B = -10 + 6
B = -4.
So the numbers are
A = -10, B = -4, C = 8, D = 49, E = 50.
Edwin
and larger than 8, for D and E.
perfect squares: 9, 16, 25, 36, 49
perfect squares plus1: 10, 17, 26, 37, 50
Let's try D = 49 in (4)
D = 199-3E
49 = 199-3E
3E = 150
E = 50
and E=50 is one of those "perfect square + 1's, namely 1 more than 49, or D.
So I think we have it.
Substitute D = 49 and E = 50 in (2)
(2) E-60 = A
50-60 = A
-10 = A
and substituting in (1)
B = A+6
B = -10 + 6
B = -4.
So the numbers are
A = -10, B = -4, C = 8, D = 49, E = 50.
Edwin