|
Question 520556: it takes 5 workers 9 days to build a barn? how many days would it take 3 workers to build a barn?
extra credit:
if a the barn needs to be build in 7 days, what is the number of workers needed?
Found 2 solutions by oberobic, bucky:
Answer by oberobic(2304)   (Show Source): (Show Source):
You can put this solution on YOUR website! With job problems like this, it is best to look at the problem as a question of fractions.
.
a crew of 5 workers can build a barn in 9 days
the crew builds 1/9 of the barn per day
each worker is 1/5 of the crew
each worker builds 1/45 of the barn per day
.
5 workers * 1/45 barn/day * 9 days = 45/45 barn = 1 barn
.
3 workers * 1/45 barn/day * x days = 1 barn
3 * 1/45 * x = 1
3/45*x = 1
3x = 45
x = 15 days
.
Done.
Answer by bucky(2189)   (Show Source): (Show Source):
You can put this solution on YOUR website! Another tutor has given you a good explanation of the team effort it takes for 5 men finishing the job in 9 days. Each man does  of the job per day. In that way, if the team consists of just 3 men, it takes that team 15 days to do the job. of the job per day. In that way, if the team consists of just 3 men, it takes that team 15 days to do the job.
.
That being the case, for the extra credit part:
.
If the job needs to be done in 7 days, each day the team of "x" number of men needs to do  of the job each day. Since each team member does of the job each day. Since each team member does  of the job in a day, if you multiply that times the unknown number of men, the answer must equal of the job in a day, if you multiply that times the unknown number of men, the answer must equal  . In equation form this can be written as: . In equation form this can be written as:
.

.
You can solve this equation for "x" by multiplying both sides of the equation by 45 as follows:
.

.
On the left side the multiplier of 45 cancels with the denominator and you are left with:
.

.
When you divide out the right side you get the answer 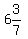 . .
.
Since 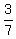 of a person is not realistic, 6 men will NOT complete the job in 7 days. Therefore, 7 men will complete the job before the end of the 7th day. of a person is not realistic, 6 men will NOT complete the job in 7 days. Therefore, 7 men will complete the job before the end of the 7th day.
.
Consider this ... 7 men, each doing  of the job per day will complete of the job per day will complete 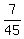 of the job per day. Therefore, is 7 days they will do of the job per day. Therefore, is 7 days they will do  of the job. This tells you that in 7 days they will complete of the job. This tells you that in 7 days they will complete  of the job ... in other words the 7 man team in 7 days will have the capability to complete the 1 job and do a little more work on another job too. of the job ... in other words the 7 man team in 7 days will have the capability to complete the 1 job and do a little more work on another job too.
.
Hope this helps you score the extra credit.
|
|
|
| |