SOLUTION: 1)consider the polynomial p(x)=x^3+ax^2+bx-12 given that (x+3)and (x-4)are factors of p(x), factorise p(x)completely. 2)the polynomial p(x)=2x^3-ax^2=bx+48 has (x-4) as a repea

Assume that the other factor of p(x) is x-r.  Then

p(x) = x³ + ax² + bx - 12 = (x + 3)(x - 4)(x - r) = (x² - x - 12)(x - r) =

x³ - rx - x² + rx - 12x + 12r

x³ + ax² + bx - 12 = x³ - rx² - x² + rx - 12x + 12r

x³ + ax² + bx - 12 = x³ - (r + 1)x² + (r - 12)x + 12r

Equate coefficients of like powers of x:

a = -(r + 1)
b = (r - 12)
-12 = 12r which tells us that r = -1

a = -(r + 1) = -(-1+1) = 0
b = (r - 12) = -1 - 12 = -13

p(x) = x³ + ax² + bx - 12 = (x + 3)(x - 4)(x - r) = 

(x + 3)(x - 4)[x -(-1)] =

(x + 3)(x - 4)(x + 1)

Assume that the factors are (x - 4), (x - 4), (x - r), and 2.

Then

p(x) = 2x³ + ax² + bx - 12 = (x - 4)(x - 4)2(x - r)

Notice that I put in the factor 2 because the first coefficient is 2
and that 2 is necessary to make the terms in x³ the same.


p(x) = (x - 4)(x - 4)2(x - r)

Multiply that all the way out and get

p(x) = 2x³ + ax² + bx - 12 
= 2x³ - 2rx² - 16x² + 16rx + 32x - 32r =
2x³ + (-2r-16)x² + (16r+32)x - 32r 

Now equate the coeficcients of

2x³ + ax² + bx - 12

and

2x³ + (-2r-16)x² + (16r+32)x - 32r

Equating the coefficients of x²:

a = -2r - 16

Equating the coefficients of x

b = 16r + 32

Equating the constant term:

-32r = -12

Solving for r:

r = 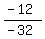 = {{3/8}}}

Substituting r =  in

b = 16r+32
b = 16()+32
b = 38

Substituting r =  in

a = -2r - 16
a = -2 - 16
a =  - 16
a =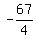 

So all you want is a =  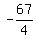and b = 38.

Checking: the polynomial function you want is 

p(x) = 2x³ + 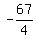x² + 38x - 12

and it "factorises" [We say "factors" in the US, we don't say "factorises",
like we say "color", "flavor" and "center", not "colour", "flavour", and "centre"] :)
as:

p(x) = (x - 4)(x - 4)2(x - r)

p(x) = (x - 4)(x - 4)2(x - )

p(x) = (x - 4)²(2)(x - )

or you can multiply the 2 into the parentheses
that follows it and get

p(x) = (x - 4)²(2x - )

Or maybe you want to get a least common
denominator in the parentheses:

p(x) = (x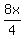 - 4)²( - )

p(x) = (x - 4)²()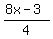

and put the  out in front and get:

(x - 4)²(8x - 3)

The graph of p(x) is given below:



Edwin