Question 51968: I am not sure if I am getting the right answer for this problem. I need a little help.
For the equation x - the square root of x = 0, perform the following:
Solve for all values of x that satisfies the equation
Graph the functions y = x and y = the square root of x on the same graph (by plotting points if necessary). Show the points of intersection of these two graphs.
I am not sure how to graph this function. Thanks for your time.
Answer by funmath(2933)   (Show Source):
You can put this solution on YOUR website!  can be solved algebraically a couple of different ways. I showed another student one way to solve it earlier today. Look it up and I'll show you a second way to do it.
 (add  to both sides)
 (simplify)
 (square both sides)
 (subtract x from both sides)
 (factor out an x)
x=0 and x-1=0 (zero product property)
x=0 and x-1+1=0+1
x=0 and x=1
Because this involves a square root you'll need to check for false solutions called extraneous solutions by substituting the answers back into the original equations to make sure they work.
0-0=0
1-1=0
Both x=0 and x=1 are valid solutions.
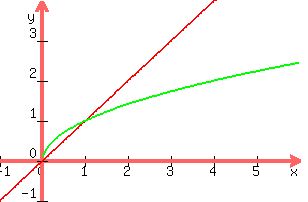
As for the graphing:
y=x is a line, you can substitute values for x and get coordinates for points to connect.
When x=0, y=0 gives you the coordinate (0,0)
When x =1, y=1 (1,1)
When x=2, y=2 (2,2)
For 
When x=0, 
y=0 (0,0)
When x=1, 
y=1 (1,1)
When x=4, 
y=2 (4,2)
When you plot all those points, you'll see that the two graphs intersect at x=0 and x=1. This verifies our algebraic answer.
Happy Calculating!!!
|
|
|
