We first will find the number of non-decreasing sequences of 5 digits with
product 720. Then we will rearrange them.
Since 720 is divisible by 5 only once, the digit 5 must be included once
in them all.
That means the remaining 4 digits must have product 720÷5 or 144.
So the problem is now reduced to finding the number non-decreasing sequences of
4 digits with product 144.
We cannot have more than one 1 because in the extreme case
the product 1*1*9*9 is only 81.
1. Cases when we the 1st digit of the non-decreasing sequence is 1:
This problem reduces to finding non-decreasing sequences of 3 digits with
product 144
If we use 2 as the 2nd digit, the remaining digits must have product 72,
so they have to be 8 and 9, so we have only the non-decreasing sequence
{1,2,8,9} with product 144.
If we use 3 as the 2nd digit, the remaining digits must have product 48,
so they have to be 6 and 8 so we have the non-decreasing sequence of
{1,3,6,8} with product 144.
If we use 4 as the 2nd digit, the remaining digits must have product 36,
so they have to be 4 and 9 or 6 and 6, so we have the set of digits
{1,4,4,9} and {1,4,6,6}
So there are these 4 sets of non-decreasing sequences of 4 digits whose
product is 144 which begin with 1.
(1,2,8,9), {1,3,6,8}, {1,4,4,9}, and {1,4,6,6}
2. If we use 2 as the first digit,
then the remaining 3 digits must have
product 72.
If the 2nd digit of the sequence is 2, the 3rd and 4th digits
must have product 36, so we have sequences (2,2,4,9) and (2,2,6,6)
If the 2nd digit of the sequence is 3, the 3rd and 4th digits
must have product 24, so we have sequences (2,3,3,8) and (2,3,4,6)
So for sequences beginning with 2,
(2,2,4,9), (2,2,6,6), (2,3,3,8), and (2,3,4,6)
3. If we use 3 as the first digit,
Then the remaining 3 digits must have product 48
If the 2nd digit of the sequence is 3, the remaining 2 digits must
have product 16, thus we have only the sequence (3,3,4,4)
None can begin with 4 because 4*4*4*4 = 256, which is larger than 144.
So the only non-decreasing sequences of digits which have product 144
are these 9
(1,2,8,9)
(1,3,6,8)
(1,4,4,9)
(1,4,6,6)
(2,2,4,9)
(2,2,6,6)
(2,3,3,8)
(2,3,4,6)
(3,3,4,4)
Now we insert the 5 in each one, and we have
(1,2,5,8,9)
(1,3,5,6,8)
(1,4,4,5,9)
(1,4,5,6,6)
(2,2,4,5,9)
(2,2,5,6,6)
(2,3,3,5,8)
(2,3,4,5,6)
(3,3,4,4,5)
Now we must arrange these into all possible 5-digit numbers:
The ones which have no repeated digits are
(1,2,5,8,9), (1,3,5,6,8), (2,3,4,5,6)
Thus they account for 3*5! numbers with product of digits 720
The ones with 1 pair of repeated digits are
(1,4,4,5,9), (1,4,5,6,6), (2,2,4,5,9), (2,3,3,5,8)
They account for 4*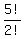 numbers with product of digits 720
The ones with 2 pairs of repeated digits are
(2,2,5,6,6), (3,3,4,4,5)
They account for 2*
numbers with product of digits 720
The ones with 2 pairs of repeated digits are
(2,2,5,6,6), (3,3,4,4,5)
They account for 2*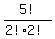 numbers with product of
digits 720.
So the grand total is
3*5! + 4*
numbers with product of
digits 720.
So the grand total is
3*5! + 4*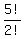 + 2*
+ 2*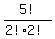 360 + 240 + 60 = 660.
That's the answer, 660.
Edwin
360 + 240 + 60 = 660.
That's the answer, 660.
Edwin