(x+16)(x-8)(x+10) > 0
We find all the critical values by setting the left side = 0
(x+16)(x-8)(x+10) = 0
x+16=0; x-8=0; x+10=0
x=-16 x=8 x=-10
We plot those critical values on a number line:
--------o-----o-----------------o--------
-16 -10 8
We choose a test value in each of the 4 intervals those
critical points divide the number line into:
In the interval left of -16, we choose -17 as a test point:
Substitute -17 in the original inequality:
(x+16)(x-8)(x+10) > 0
(-17+16)(-17-8)(-17+10) > 0
(-1)(-25)(-7) > 0
-175 > 0
That is false, so we DO NOT shade the interval to the left of -16
So we still have an empty number line:
--------o-----o-----------------o--------
-16 -10 8
In the interval between -16 and -10, we choose -11 as a test point:
Substitute -11 in the original inequality:
(x+16)(x-8)(x+10) > 0
(-11+16)(-11-8)(-11+10) > 0
(5)(-19)(-1) > 0
95 > 0
That is true, so we shade the interval between -16 and 10.
--------o=====o-----------------o--------
-16 -10 8
In the interval between -10 and 8, we choose 0 as a test point:
Substitute 0 in the original inequality:
(x+16)(x-8)(x+10) > 0
(0+16)(0-8)(0+10) > 0
(16)(-8)(10) > 0
-1280 > 0
That is false, so we DO NOT shade the interval between -10 and 8.
So we still have:
--------o=====o-----------------o--------
-16 -10 8
In the interval right of 8, we choose 9 as a test point:
Substitute 9 in the original inequality:
(x+16)(x-8)(x+10) > 0
(9+16)(9-8)(9+10) > 0
(25)(1)(19) > 0
475 > 0
That is true, so we shade the interval right of 8:
--------o=====o-----------------o=======>
-16 -10 8
So the solution set is
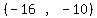 ⋃
⋃ 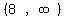 Edwin
Edwin