|
Question 519071: two lines, AB and CD, intersect at point E. find the values of x and y given that: the measure of angle AED equals (10x+9y), the measure of angle AEC equals (xy), and the measure of angle CEB equals (15x).
Answer by ankor@dixie-net.com(22740)   (Show Source): (Show Source):
You can put this solution on YOUR website! two lines, AB and CD, intersect at point E.
find the values of x and y given that:
the measure of angle AED equals (10x+9y), the measure of angle AEC equals (xy), and the measure of angle CEB equals (15x).
:
We know AED = CEB, therefore
10x + 9y = 15x
9y = 15x - 10x
9y = 5x
:
We know AEC + CEB = 180 degrees, therefore
xy + 15x = 180
xy = 180 - 15x
divide by x
y =  - 15 - 15
replace y with this in the 1st equation
9( - 15) = 5x - 15) = 5x
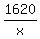 - 135 = 5x - 135 = 5x
simplify, divide by 5
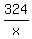 - 27 = x - 27 = x
multiply both sides by x, results
324 - 27x = x^2
Arrange as a quadratic equation on the right
0 = x^2 + 27x - 324
You can use the quadratic formula but this will factor to:
(x+36)(x-9) = 0
positive solution
x = 9
Find y
9y = 5x
9y = 5(9)
9y = 45
y = 45/9
y = 5
:
You can use x=9, y=5 to find the measure of the angles, and confirm that the angle conform the rules of intersecting lines
|
|
|
| |