Although there are many normal curves, they all share an important property
that allows us to treat them in a uniform fashion.
The 68-95-99.7% Rule
All normal density curves satisfy the following property which is often
referred to as the Empirical Rule.
approximately 68%
of the observations fall within 1 standard deviation of the mean, that is,
between 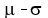 .
approximately 95%
of the observations fall within 2 standard deviations of the mean, that is,
between
.
approximately 95%
of the observations fall within 2 standard deviations of the mean, that is,
between 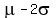 .
approximately 99.7%
of the observations fall within 3 standard deviations of the mean, that is,
between
.
approximately 99.7%
of the observations fall within 3 standard deviations of the mean, that is,
between 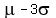 .
Thus, for a normal distribution, almost all values lie within 3 standard
deviations of the mean.
Below are the percentages of observations that fall between
the intervals:
.
Thus, for a normal distribution, almost all values lie within 3 standard
deviations of the mean.
Below are the percentages of observations that fall between
the intervals:
 3. The weights of men are normally distributed with a mean of 200 pounds
and a standard deviation of 25 pounds.
So let's calculate the values on the x-axis:
3. The weights of men are normally distributed with a mean of 200 pounds
and a standard deviation of 25 pounds.
So let's calculate the values on the x-axis:






 and re-draw the figure with these values:
and re-draw the figure with these values:
 a. Find the percent of men with weights between 175 pounds and 225 pounds.
Add the percentages in the graph above in the two regions
between 175 and 225: 34.134% + 34.134% = 68.268%. Or use the 68-95-97.5
rule and get about 68% because 175 =
a. Find the percent of men with weights between 175 pounds and 225 pounds.
Add the percentages in the graph above in the two regions
between 175 and 225: 34.134% + 34.134% = 68.268%. Or use the 68-95-97.5
rule and get about 68% because 175 =  and 225 =
and 225 =  .
b. Among 100 men how many are expected to weigh
1) Between 175 pounds and 225 pounds?
Since that's about 68%, we find that 68% of 100 men is 68 men.
b. Among 100 men how many are expected to weigh
2) Less than or equal 200 pounds?
One way is to add the percentages in the graph above in all the regions
to the left of the mean: 0.135%+2.140%+13.591%+34.134% = 50%.
Another way is to just observe that half or 50% are below the mean.
Either way, 50% of 100 men is 50 men
b. Among 100 men how many are expected to weigh
3) Greater than equal 250 pounds?
I think you might have meant this one to be 250 instead of 240, so I
chnaged it to 250. To do it for 240 pounds involves z-scores and a
normal table, and since the other ones just required the 68-95-99.7%
rule, I'll assume you meant this to be 250, not 240. so we add the
percentages in the two regions the the right of 250 which are
2.140%+0.135% = 2.275% and 2.275% of 100 men is 2.275 men, but sinch
we can't cut men into fractions, we round to about 2 men.
Now if you did mean 240, then the z-score is 1.6, and so you look up
z=1.6 in the z-table you either find 0.4452 or 0.9452, depending on
which type of tabel you are using.
If you found 0.4452, you subtract 0.5-0.4452 = 0.0548
If you found 0.9452, you subtract 1.0-0.4452 = 0.0548
So if it really is 240 and not 250, then the answer is about
5.48% of 100, or 5.48 which rounds to about 5 men.
Edwin
.
b. Among 100 men how many are expected to weigh
1) Between 175 pounds and 225 pounds?
Since that's about 68%, we find that 68% of 100 men is 68 men.
b. Among 100 men how many are expected to weigh
2) Less than or equal 200 pounds?
One way is to add the percentages in the graph above in all the regions
to the left of the mean: 0.135%+2.140%+13.591%+34.134% = 50%.
Another way is to just observe that half or 50% are below the mean.
Either way, 50% of 100 men is 50 men
b. Among 100 men how many are expected to weigh
3) Greater than equal 250 pounds?
I think you might have meant this one to be 250 instead of 240, so I
chnaged it to 250. To do it for 240 pounds involves z-scores and a
normal table, and since the other ones just required the 68-95-99.7%
rule, I'll assume you meant this to be 250, not 240. so we add the
percentages in the two regions the the right of 250 which are
2.140%+0.135% = 2.275% and 2.275% of 100 men is 2.275 men, but sinch
we can't cut men into fractions, we round to about 2 men.
Now if you did mean 240, then the z-score is 1.6, and so you look up
z=1.6 in the z-table you either find 0.4452 or 0.9452, depending on
which type of tabel you are using.
If you found 0.4452, you subtract 0.5-0.4452 = 0.0548
If you found 0.9452, you subtract 1.0-0.4452 = 0.0548
So if it really is 240 and not 250, then the answer is about
5.48% of 100, or 5.48 which rounds to about 5 men.
Edwin