SOLUTION: find the vertex, the line of symetry, and the maximum or minimum value of f(x). graph f(x)=1/3(x+5)^2+6 vertex= line of symetry= max/min value= is it max or min= graph

Rules:

For f(x) = a(x-h)² + k

vertex = (h,k)

line of symetry = the line whose equation is x = h, a vertical line
through h on the x-axis: 

max/min value = k 

Is it max or min = max?  Rule: if a > 0 it is a min, if a < 0, it is
a max.  

To draw the graph:  

1. Draw the line of symmetry.
2. Plot the vertex (h,k), 
3. Plot the two points (h+1,k+a), (h-1,k+a)
4. Draw a u-shaped curve through them, symmetrical about the line
of symmetry.

-------------------------------
Use the rule on your equation:

f(x) = (x+5)² + 6

Compare to:

f(x) = a(x-h)² + k

a = , h = -5, k = 6

vertex = (h,k) = (-5,6)

line of symetry = the line whose equation is x = h, or x = -5 

max/min value = k = 6 

Is it max or min = max?  Rule: if a > 0 it is a min, if a < 0, it is
a max.   Since a =  which is > 0, it is a min.
  
To draw the graph:  

1. Draw the line of symmetry, a vertical line through -5 on the x-axis,
whose equation is x = -5





2. Plot the vertex (h,k) = (-5,6)






3. Plot the two points (h+1,k+a) = (-5+1,6+) = (-4,)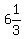
and (h-1,k+a) = (-5-1,6+) = (-6,)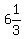



4. Draw a u-shaped curve through them, symmetrical about the line
of symmetry.



Edwin