We are to prove
if x5=x4+1, then x³=x+1
or
if x5-x4-1=0, then x³-x-1=0
or we are to prove:
if f(x) = x5 - x4 - 1 = 0 and g(x) = x³ - x - 1 = 0
then all zeros of f(x) are zeros of g(x).
This is likely not true for all complex zeros of f(x), since a 5th degree
polynomial has 5 zeros (counting multiplicities) whereas a 3rd degree
polynomial has only 3. However it may be true for x real.
Let's consider the case when x is a real number.
By Descartes' rule of signs, both f(x) and g(x) have 1 positive zero.
f(x) has no negative solutions. g(x) either has 2 or no negative zeros.
They could have the same positive zero if g(x) were a factor of f(x).
So we see if this is the case by long division of f(x)÷g(x):
x² - x + 1
x³ + 0x² - x - 1)x5 - x4 + 0x³ + 0x² - 0x - 1
x5 + 0x4 - x³ - x²
-x4 + x³ + x² - 0x
-x4 - 0x³ + x² + x
x³ + 0x² - x - 1
x³ + 0x² - x - 1
0
Yes indeed we get a 0 remainder, so
x5-x4-1 = (x³-x-1)(x²-x+1)
f(x) = g(x)·(x²-x+1)
x²-x+1 has only conjugate complex imaginary zeros 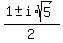 , so if
x = the one and only real zero of f(x), the right side is also 0, and x²-x+1 is
not 0 since it has only imaginary zeros
, so if
x = the one and only real zero of f(x), the right side is also 0, and x²-x+1 is
not 0 since it has only imaginary zeros 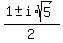 , so x must also
be the real zero of g(x). So the proposition is true for x real.
However it is not true for x complex imaginary, for the zeros
, so x must also
be the real zero of g(x). So the proposition is true for x real.
However it is not true for x complex imaginary, for the zeros
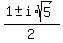 of x²-x+1 are zeros of f(x), but are not zeros of g(x).
Edwin
of x²-x+1 are zeros of f(x), but are not zeros of g(x).
Edwin