I'll just do the second one, the only one with a
fraction solution:
{ x + 3y = 11
{4x - 3y = -2
To eliminate the x's multiply the first equation through
by -4, so that its first term will become -4x and will
cancel with the 4x in the second equation:
-4x - 12y = -44
4x - 3y = -2
Now when we add them term by term vertically we get:
-4x - 12y = -44
4x - 3y = -2
---------------
-15y = -46
y = 
y = 
Now to eliminate the y's, we don't need to
multiply either one through because the terms
in y are already opposite and will cancel just
as they are. So we add term by term vertically:
{ x + 3y = 11
{4x - 3y = -2
-------------
5x = 9
x = 
Solution is (x,y) = 
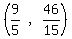Here are the solutions to the others. You can solve them similar
to the way I solved the second one:
{-x+3y=-1
{x-2y=2 BY elmination: Solution is (x,y) = (4,1)
{x+y=7
{x+3y=11 by elmination: Solved above.
{4x-3y=-2
{4x+5y=14 by elmination: Solution is (x,y) = (1,2)
{x+2y=10
{3x-y=9 By elmination Solution is (x,y) = (4,3)
Edwin
