Question 515307: A bank has a test designed to establish the credit rating of a loan applicant. Of the persons, who default (D), 90% fail the test (F). Of the persons, who will repay the bank (ND), 5% fail the test. Furthermore, it is given that 4% of the population is not worthy of credit; i.e., P(D) = .04. Given that someone failed the test, what is the probability that he actually will default (When given a loan
Answer by drcole(72)   (Show Source): (Show Source):
You can put this solution on YOUR website! This is a conditional probability question. We know the following:
P(D) = 0.04 = the probability of default in the population as a whole;
P(ND) = 0.96 = the probability of non-default in the population as a whole, since the person can either default (D) or not default (ND), so we know that P(D) + P(ND) = 1;
P(F|D) = 0.90 = the conditional probability of failing the test, given that a person defaulted (i.e., if we already know that the person defaulted, there is a 90% chance that they failed the test; and
P(F|ND) = 0.05 = the conditional probability of failing the test, given that a person did not default (i.e., if we already know that the person did not default, there is only a 5% chance that they failed the test.
We want to know the conditional probability that someone defaults, given that we know they failed the test. In probability notation, this is P(D|F).
Recall that the conditional probability of an event E, given we know that an event F is true, is given by the formula (where P(A|B) is written "P(A given B)":

So to compute P(D|F), we want to know P(D and F) and P(F). To find P(D and F), we solve using the above formula and P(F|D):
 (applying the conditional probability formula to P(F|D)) (applying the conditional probability formula to P(F|D))
 (substituting for P(F|D) and P(D)) (substituting for P(F|D) and P(D))
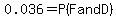 (multiplying both sides by 0.04) (multiplying both sides by 0.04)
So P(D and F) = P(F and D) = 0.036. Now we need to find P(F). One way to do this is to realize that, if someone fails the test and takes out a loan, they will either default or not default: they cannot do both or neither. So the probability of failing the test equals the sum of the probability of failing the test and defaulting, and the probability of failing the test and not defaulting:
P(F) = P(F and D) + P(F and ND)
So if we know P(F and ND), since we already know P(F and D), we can figure out P(F). We can find P(F and ND) using the same method as for P(F and D), using P(F|ND) instead:
 (applying the conditional probability formula to P(F|ND)) (applying the conditional probability formula to P(F|ND))
 (substituting for P(F|ND) and P(ND)) (substituting for P(F|ND) and P(ND))
 (multiplying both sides by 0.96) (multiplying both sides by 0.96)
Now we can find P(F):

Thus we can finally finish the problem:

So, to the nearest thousandth, the conditional probability of defaulting on a loan, given that a person has failed the test, is 0.409. This makes more sense that it looks at first: remember that 5% of the non-defaulters failed the test, and non-defaulters make up 96% of the population. Because most people are non-defaulters, a large percentage of those who fail the test are going to be false positives.
|
|
|