Question 515227: A machine Shop has 100 drill presses and other machines in constant use. The probablility that a machine will become inoperative during a given day is .002. During some days no machines are inoperative, but during some days one, two three or more are broken down.
a. what type of distribution is this?
b. What is the probability that fewer than 2 machines will be inoperative during a particular day?
Answer by drcole(72)   (Show Source): (Show Source):
You can put this solution on YOUR website! a) This is a Poisson distribution. In general, a Poisson distribution tells us the probability that exactly k events happen in a given time period, given that we expect  of those events during that time period, and the chances of two or more events occurring are independent of each other. of those events during that time period, and the chances of two or more events occurring are independent of each other.
b) For a Poisson distribution as described above, the probability of exactly k events during the given time period is:

In this case, our time period is one day, we have 100 machines in use, and the probability of any given machine being inoperative on any given day is 0.002 (and the probabilities of any two machines being inoperative are independent). So we would expect 0.002 * 100 = 0.2 machines to be inoperative on any day (obviously, 0.2 machines cannot be inoperative --- think 2 machines inoperative every 10 days). So  . .
The probability of fewer than two machines being inoperative is equal to the probability of zero machines being inoperative plus the probability of one machine being inoperative.

Applying our formula, we get:

Substituting in for  and simplifying, we get: and simplifying, we get:
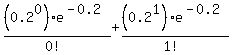 (substituting 0.2 for (substituting 0.2 for  ) )
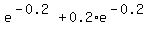 (simplifying 0! = 1, 1! = 1, and the exponents) (simplifying 0! = 1, 1! = 1, and the exponents)
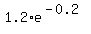 (combining like terms) (combining like terms)
So the probability of fewer than two machines being inoperative on any given day is 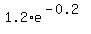 or (to the nearest thousandth) 0.982. This makes sense: if we only expect 2 machines to be inoperative every ten days, the chances of two machines being inoperative in one day should be very small. or (to the nearest thousandth) 0.982. This makes sense: if we only expect 2 machines to be inoperative every ten days, the chances of two machines being inoperative in one day should be very small.
|
|
|